基本的就不说了，CTF逆向中常见的是CRC16和CRC32

CRC-16

生成多项式: $x^{16}+x^{12}+x^{5}+1$

二进制串: 1 0001 0000 0010 0001
故HEX为 0x1 1021

计算实例

计算字符’a’的CRC16校验码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<windows.h>
//以CRC16  0x1021  为例

int main(int argc, char**argv) {
	unsigned short crc = 'a';	//计算字符a的crc16校验码
	//左移8位，和手动计算一样，相当于右边直接补了8个0
	crc <<= 8;

	//计算8次，在右边添加的 8个0 经过循环后即是结果
	for (int i = 0; i < 8; i++) {	
		//如果最高位是1的话需要计算， 如果不是直接左移(左移可以想象成补0)
         //参考手算的图示，crc左移相当于取余数进行计算
		if ((crc & 0x8000) != 0) {
			crc <<= 1;
			crc = crc ^ 0x1021;
		}
		else {
			crc <<= 1;
		}
	}
	printf("%#x", (BYTE)crc);	// 0x87
	system("pause");
	return 0;
}

这里计算字符a的CRC16校验码，仅仅给出了代码，其中细节可以参见下文以CRC-8举例的一些说明

CRC-32

生成多项式:

$x^{32}+x^{26}+x^{23}+x^{22}+x^{16}+x^{12}+x^{11}+x^{10}+x^{8}+x^{7}+x^{5}+x^{4}+x^{2}+x^{1}+1$

二进制串:1 0000 0100 1100 0001 0001 1101 1011 0111
故HEX为 0x1 04C11DB7

（另一个CRC为1 1110 1101 1011 1000 1000 0011 0010 0000 = 0x1 EDB8 8320）

一些概念

注意到，上文计算实例中，如果一开始在数据前加了一些0，对结果没有影响，因此算法有缺陷。

于是真正的应用的CRC算法都做了一些改动，增加2个概念：余数初始值、结果异或值

余数初始值，在计算CRC值的开始，给CRC寄存器一个初始值…

结果异或值，其余计算完成后将CRC寄存器的值在与这个值进行异或作为最后的校验值

CRC16: 余数初始值 0x0000 结果异或值 0x0000 （上文程序中两处0x0000没有体现）

CRC32: 余数初始值0xFFFFFFFF 结果异或值 0xFFFFFFFF

CRC-8

生成多项式有很多，这里选一种: $x^8+x^7+x^6+x^4+x^2+1$

二进制串: 1 1101 0101

故HEX为 0x1 0xD5

CRC直接移位算法(以CRC-8为例)

改进1

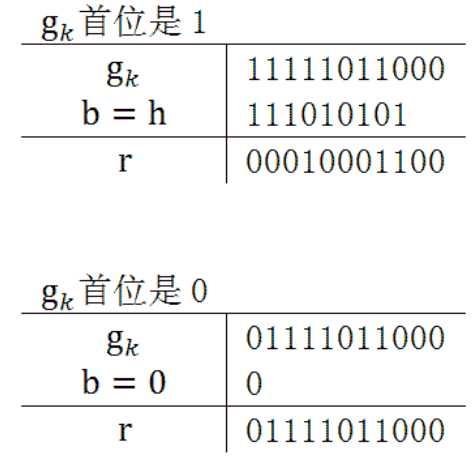
回想迭代过程，当余数首位为0时，会直接再左移一位，直到首位为1，图中$g_k$表示余数

也可以表示为，每次迭代，根据余数的首位决定与之运算的二进制码的值，记作b

若首位为1，b为hex(1021)；若首位为0，b为0

改进2

每次迭代，$g_k$的首位将会被移除（根据首位决定b的值），因为生成多项式对应二进制串的首位是1，因此只需考虑第2位后计算即可，这样就可以舍弃h的首位。比如CRC-8的h是111010101，b只需是11010101

改进3

每次迭代，受到影响的是$g_k$的前m位(CRC-m)，所以构建一个m位的寄存器，此寄存器储存$g_k$的前m位。

每次迭代计算时先将S的首位抛弃，再将寄存器左移一位，同时将数据流g的下一位加入寄存器。

至于为什么要先给出代码，再给出算法分析…是因为我是写了代码才理解这个过程的

直接查表法

举个例子，将24位的数据组成1个block，这样g就被分成6个block

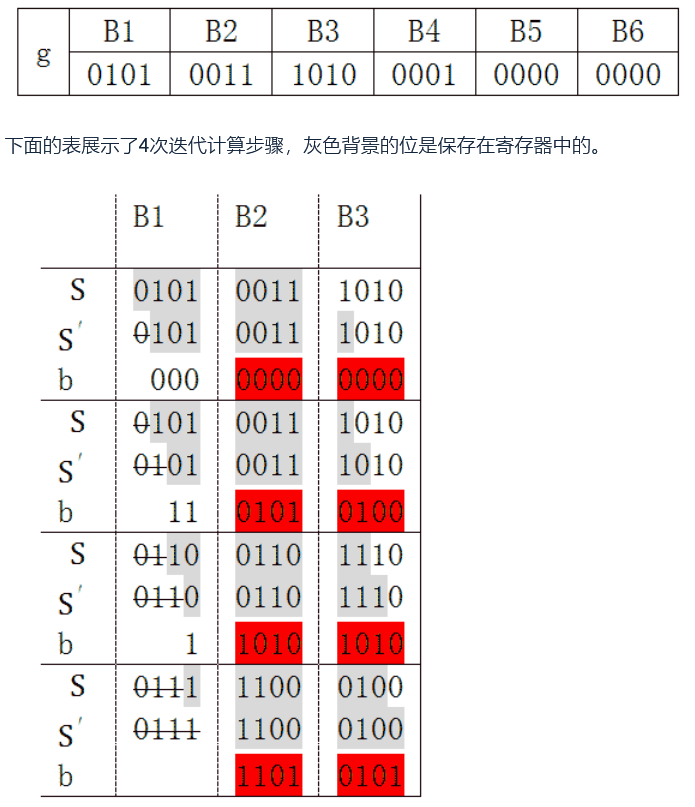
经过4次迭代，B1被移出了寄存器，这里我们只关心4次迭代对B2和B3产生了什么影响

注意表中红色部分，先给出一个定义：

B23 = 0011 1010
b1  = 0000 0000
b2  = 0101 0100
b3  = 1010 1010
b4  = 1101 0101
b'  = b1 xor b2 xor b3 xor b4

4次迭代对B23来说，实际是与b1,b2,b3,b4进行了异或运算

即 B23 = B23 xor b1 xor b2 xor b3 xor b4 ，亦即 B23 = B23 xor b'

根据XOR性质，因此CRC运算满足结合律和交换律

解释

~~关于上面那张带红色的图，我TM看了半天才看懂是什么意思~~

图中模拟了4次迭代的过程，每次右移一位，S’相较S被划去了首位。b的值始终是前八位（和红色没关系），并且取值只有2种：00000000和11010101，$b_1,b_2,b_3,b_4$才是红色的那块。

如果B1的第一位为1，那么b为11010101000(11位)，则$b_1$ (红)为b的后8位也就是10101000；若B1第一位为0则b1为00000000，也就是说，b1由B1的第一位决定。

同理，$b_2$到$b_4$也是由B1的剩下三位决定的，注意第k+1层的S是由第k层的S’和b生成的，也就是说，根据B1四位决定的$b_1$到$b_4$，S初值中的B23 = B23 xor b1 xor b2 xor b3 xor b4。既然$b_1$到$b_4$是由B1的16种情况可以确定下来的，那么根据B1就可以求出b’，其中b' = b1 xor b2 xor b3 xor b4，于是可以建表，省去这四次迭代过程而直接使B23 xor b了。

到这里我才理解了各种博客出现的这句话….

b2是由B1迭代1次后的第2位决定（既是由B1的第1和第2位决定），同理,b3和b4都是由B1决定

TMD直接说 b2由B1的第二位决定不就好了嘛…

CRC-32 直接查表法代码实现

CRC-8中，B1 B2 B3都是4bits，这表明B2+B3的8bits最终需要异或的值由B1的4bits决定；

推广到CRC-32，B1 B2 B3都应该是16bits，表明B2+B3的32bits最终需要异或的值由B1的16bits决定。

CRC-8的table中有$2^4$个数据，那么CRC-32的table中有$2^8=256$个数据。

这也是CRC-32中一次性处理4字节数据的原因（CRC-8一次处理8个bits也就是1字节）

还有很多没搞清楚的地方，想弄清楚整个发展历程实在是太困难了

逆向 CRC-m