先介绍一些相关背景
本文的部分标题按照“提出问题,描述背景理论,解决问题”来设置
欧拉乘积公式
zeta函数和素数间的第一个联系由欧拉发现,n为自然数,p为素数
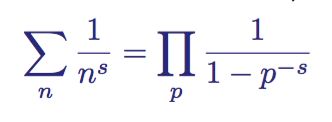
欧拉首先从一般的zeta函数开始
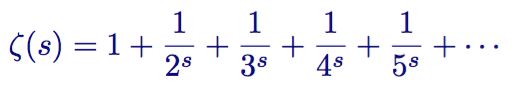
将等式两边同时乘以第二项
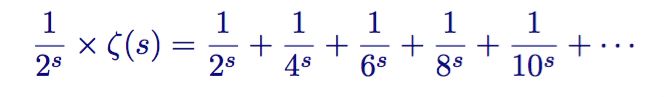
接着从zeta函数中减去结果表达式
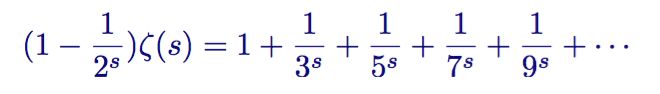
继续下去
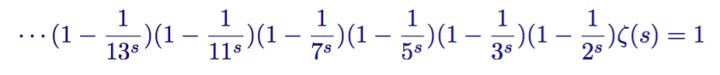
这个不难推导,类似”筛法”,最终结果如下
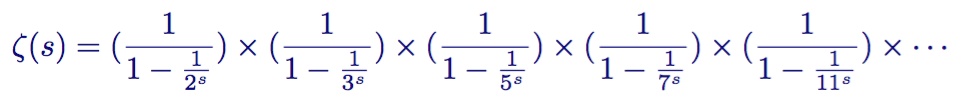
欧拉实际上构造了一个筛子,它和埃拉托斯特尼筛法很像。它将非素数从 zeta 函数中筛了出去。
简化后就得到了一开始的等式
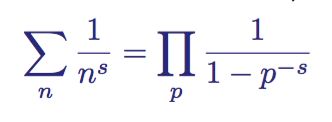
该恒等式展示了素数与zeta函数间的联系
将s = 1代入,就得到了无限调和级数,再次证明了素数的无限性
这里要说明的一点,s>1才成立,因为是收敛的,才可以当作一个正常的数运算,比如乘以一个数,否则就可能发生各种奇奇怪怪的错误
两个自然数互质的概率
可以这样思考,首先考虑两个自然数有公约数2的概率,等价于都可以表示成$ 2n $ ,最终概率也就是$ 1-\frac{1}{2^2} $
以此类推,两个自然数不存在公约数3的概率就是$ 1-\frac{1}{3^2}$
最后,两个自然数互质,等价于他们既没有公约数2,也没有3,也没有5等等
因此,互质概率等于上面所有概率的乘积
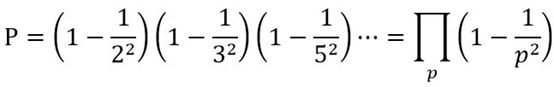
一涉及无穷,难免有点匪夷所思…
这个表达式,实际上就是s=2时欧拉乘积公式的右边部分,也就是$ \frac{1}{ζ(2)} $
高中时读过欧拉的事迹,简直就是神…
而根据定义,$ ζ(2) = \sum\limits_{i=1}^{\infty}{\frac{1}{i^2}} $
而右式的值等于$ \frac{\pi^2}{6} $
这个值也是欧拉算出来的,不过最初的证明不太严谨,但不失为一个美妙的证明
所以,两个自然数互质的概率是 $ \frac{6}{\pi^2} $,约等于60.79%
可以用计算机来验证一下,在1到32768之间随机取两个数的概率与理论值的差别非常小
以数值分析的眼光看,会发现这是相当粗糙的实验,在考虑全体自然数性质时,这个上限小的甚至是可笑的,但是这里可以发现,随着取样范围的增大,概率值收敛得是十分快的
补充一些
根据同样的推理,任选s个自然数,互质的概率就是$ \frac{1}{ζ(s)}$
很容易看出,s越大,s个自然数互质的概率就越大,因为某个质数刚好是s个自然数的共同质因子的可能性就越来越低了
而从ζ函数的角度考察,$ \frac{1}{n^{-s}}$当s>1时时减函数,所以对其求和也是减函数,所以ζ函数的倒数在增大,s个自然数互质的概率也越来越大
同时s为偶数时的无穷级数和是可以简单的计算出来的,并且都和$ \pi $相关,奇数就复杂了…
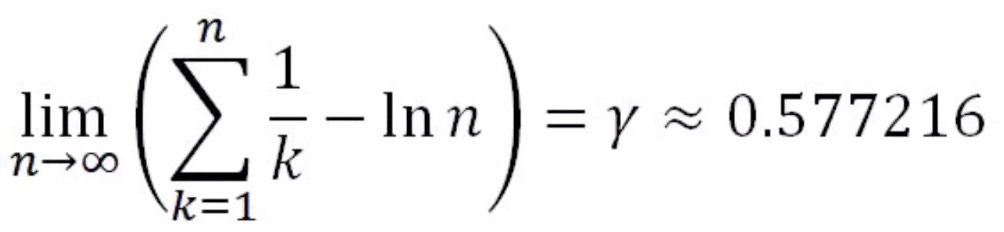
没错,又是欧拉
γ又叫做欧拉常数,为什么要说又呢
全体自然数之和
至此黎曼终于要出场了
他的基本目标是对质数的分布获得一个明确的表达式,提出了著名的黎曼猜想
同时,他的推导过程中有一个副产品甚至更有名:全体自然数之和为$ -\frac{1}{12}$
已经提到,研究质数分布的基本出发点是欧拉乘积公式
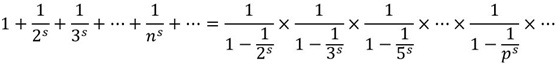
这个公式两端出现的s是一个变量,当且仅当s > 1时,欧拉乘积公式成立
黎曼提出的要点
- 我们应该把$ζ(s)$中的自变量s理解为复数,而不只是实数
- 可以通过解析延拓,让$ζ(s)$在
s < 1时也获得定义 - 通过对ζ(s)的研究,我们可以对小于等于某个数x的质数的个数给出一个明确的表达式,在这个表达式中唯一未知的就是ζ(s)的零点的位置
- 黎曼猜测,ζ(s)的零点都位于某些地方,这个猜测就是黎曼猜想
解析延拓
至此,欧拉ζ函数升级为黎曼ζ函数
假如仍然用s > 1时的定义,那么ζ(-1)就是全体自然数的和
但实际上,ζ(-1)已经换了一个定义
也就是黎曼的ζ(-1) = $ -\frac{1}{12} $
量子场论,超弦理论中经常会用到这个命题
解析延拓最基本的理解:扩大函数的定义域
例1、y=x
举个例子来直观理解,$ y = x , x∈[-1,1] $
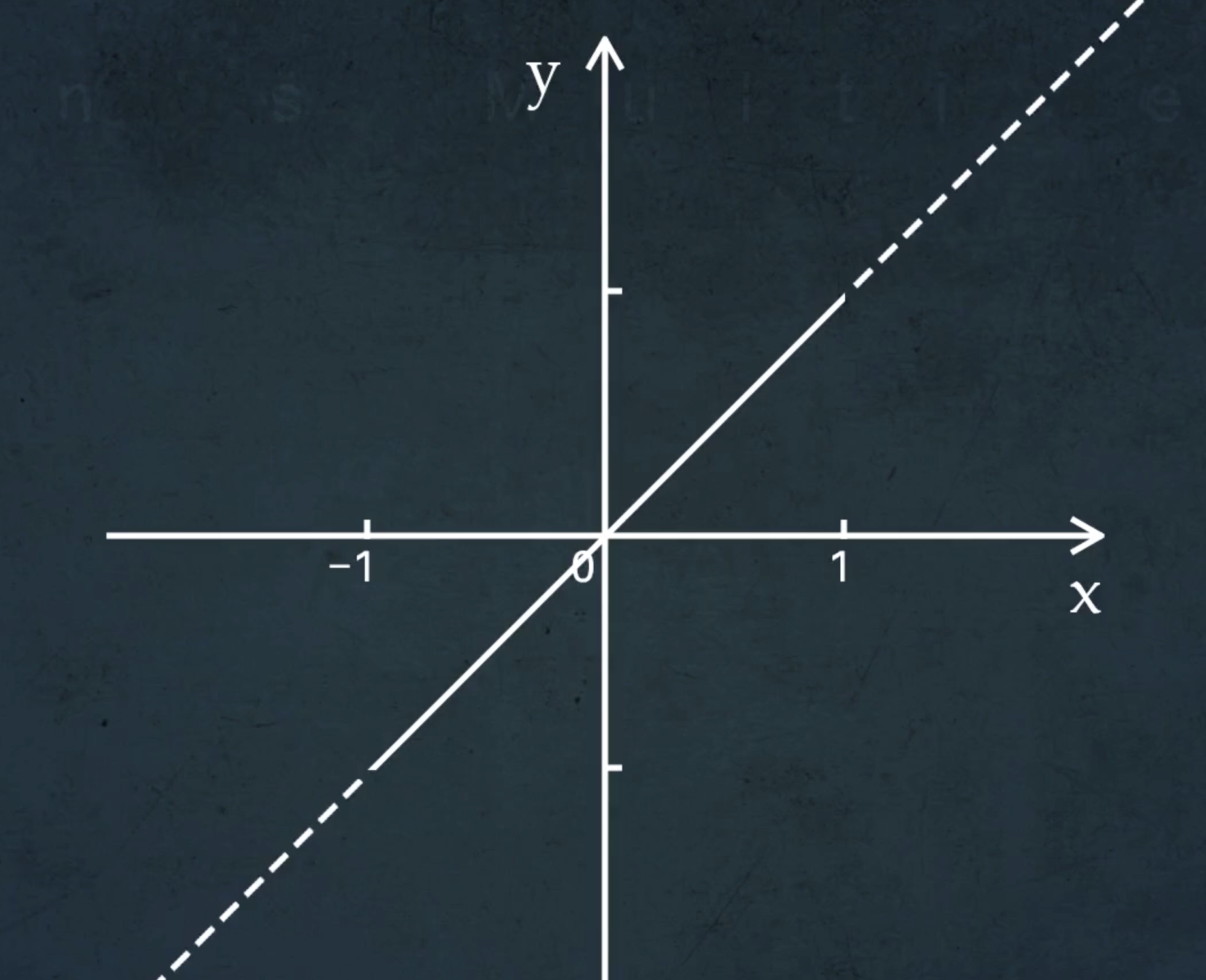
这是一条线段,我们可以任意延伸至任意远,把定义域扩展到整个数轴
但是解析延拓,重点在解析,延续了原始函数的自然趋势
所以我们不能乱延伸……
一个函数的解析延拓是唯一的
mac ctrl+A 行首 ctrl+E 行尾
一般方法:幂级数
假如一个函数$ y = f(x) $在某个点$ x_0 $附近等于一个幂级数,那么称这个函数在这一点是解析(analytic)的
这也是“解析”这个词的严格定义。
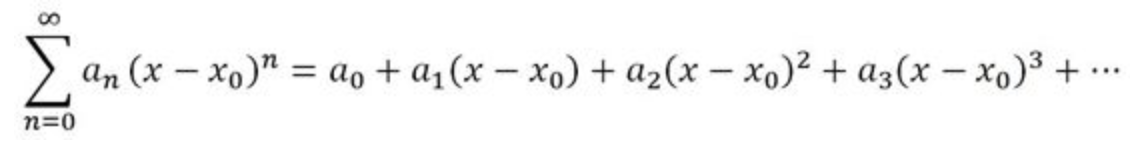
回到之前的y=x的例子,它本身就是一个幂级数,其中$ x_0 = 0 $,也就是说它在原点处等于一个幂级数,其中只有一次项的系数为1,其它都为0;当然对于原点之外的$ x_0 $仍然是一个幂级数,都是解析的
收敛半径
对于一个幂级数,一个很重要的性质是它的收敛半径(radius of convergence)
也就是说,一个幂级数并不总是收敛的,或者说并不总是能算出一个有限值
如果离中心点$ x_0 $太远,幂级数就可能变成无穷大,也就是发散了
对于 y = x,它的收敛半径是无穷大,也就是说在任何地方都收敛
例2、等比级数
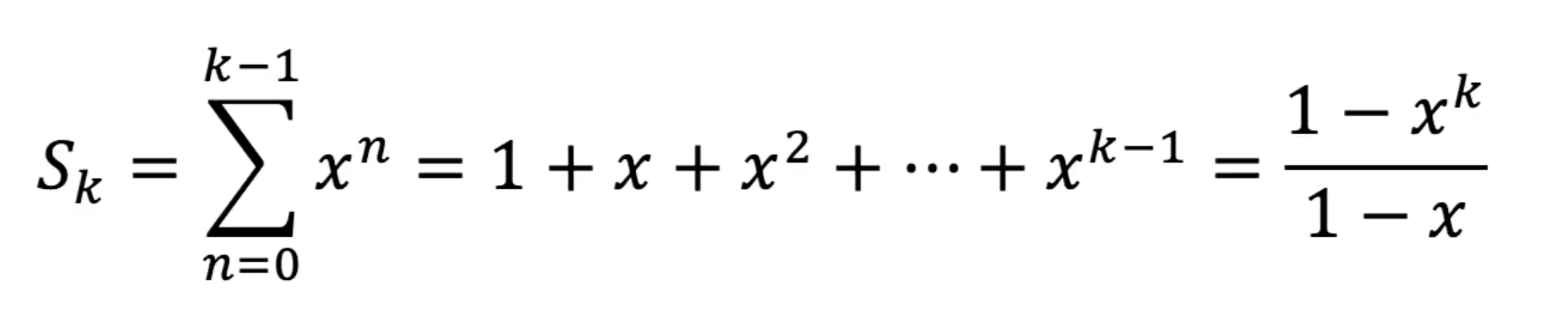
我们要求无穷多项的和,如果$ -1 < x < 1 $,则当k趋于无穷时,$ x^k $趋于0,所以求和结果会趋于$ \frac{1}{1-x} $
而若$ x > 1 $或$ x < -1 $,求和结果显然会趋于无穷大
得出结论:等比级数的收敛半径等于1,在这个收敛半径之内它等于$ \frac{1}{1-x} $,而在收敛半径之外它发散
所以等比级数的定义域最大只能到$ (-1,1) $这个区间
接着,我们对等比级数进行解析延拓
在收敛半径之外,我们定义它等于$ \frac{1}{1-x} $,这样我们就获得了一个定义域更大的函数,定义域扩大到除$ x = 1$之外的所有点
例3、格兰迪级数
接着等比级数的讨论,我们把$ x = -1 $代回等比级数中,假装不知道这时函数定义已经改变了……
在形式上得到:
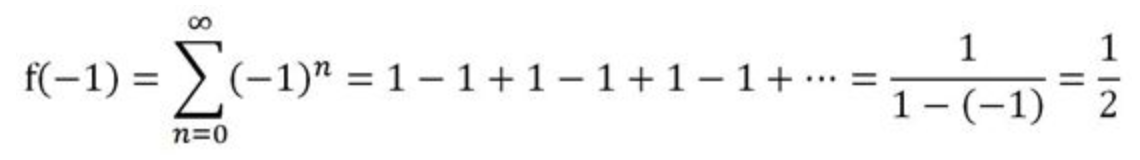
实际上,就基本的意义而言,格兰迪级数不等于任何一个数,但在某种推广的意义上,可以认为它等于$ \frac{1}{2} $
黎曼$\zeta(-1)$
有了这些背景,我们终于可以回到全体自然数之和这个正题了……
首先,欧拉$ ζ(s) $在$ s<=1 $时是发散的,因此没有意义
但是黎曼提出了一种通过$\zeta(s)$来定义$ \zeta(1-s) $的方法,使函数在$ x<0 $时也获得了定义
黎曼的函数方程
他首先非常不显然的但正确推导过程证明了以下的等式
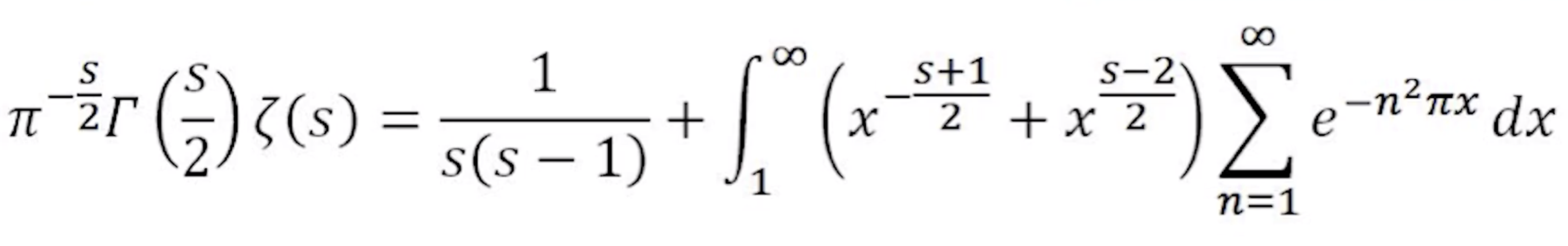
这里的$ Γ $是欧拉Gamma函数,是阶乘的扩展
最重要的一点是:右边关于s的表达式中,把s换成1-s,答案不变
因此等式左边也可以替换,因此得出:
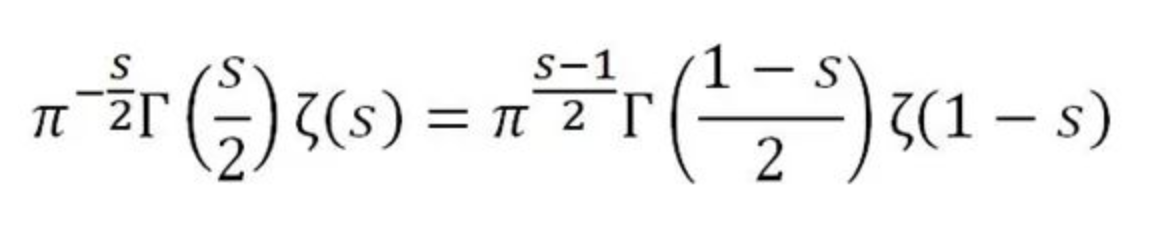
这个等式叫做黎曼的函数方程
根据这个等式,如果知道了$ \zeta(s) $,就可以算出$ \zeta(1-s) $
就这样黎曼$ \zeta $函数做出了解析延拓,从它已知的在$ s>1 $的值,可以定义它在$ s<0 $的值
狄利克雷级数
我们还会发现一个问题,定义域$ [0,1] $内该怎么办呢……
实际上在黎曼之前,已有数学家对这个区域做出了解析延拓
回顾之前,我们把$ n^{-s} $ 记作$ f(n) $,把所有$ f(n) $的和即$ f(1)+f(2)+f(3)+… $记作A
把$ f(2) $乘到A上,我们会得到所有的偶数项,当时我们从A中减去$ f(2)A$,就消去了所有的偶数项,只剩下了奇数项
现在,我们考虑从A中减去$ 2f(2)A $,结果是:
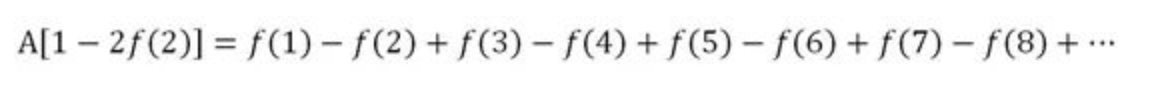
右边的表达式中,正负号交替出现,这个级数叫做狄利克雷函数(Dirichlet series)
黎曼当时就是继承了狄利克雷在哥廷根大学的职位
正是由于正负号交替出现,狄利克雷级数的收敛范围扩大了,从$ s>1 $扩大到了$ s>0 $
因此,在定义域$ [0,1] $中,$ \zeta(s) $就可以用狄利克雷函数函数除以$[1-2f(2)]$来定义
解析延拓之后
画出图像
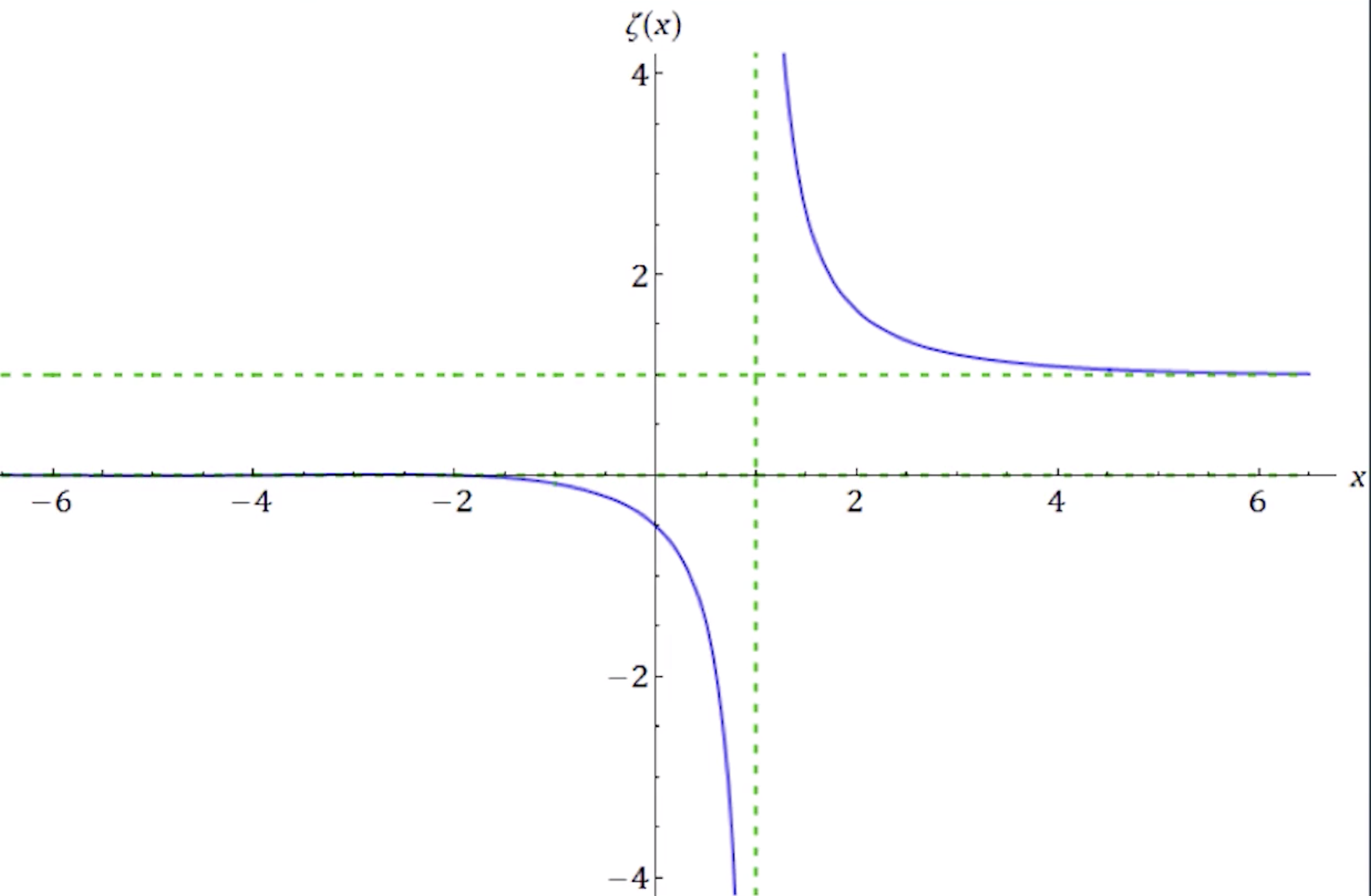
其中$s=1$仍然是无穷大
而在$s<1$的区域,我们假装不知道ζ函数的定义已经改变了,把$s>1$时的级数代入,可以得到以下结果:
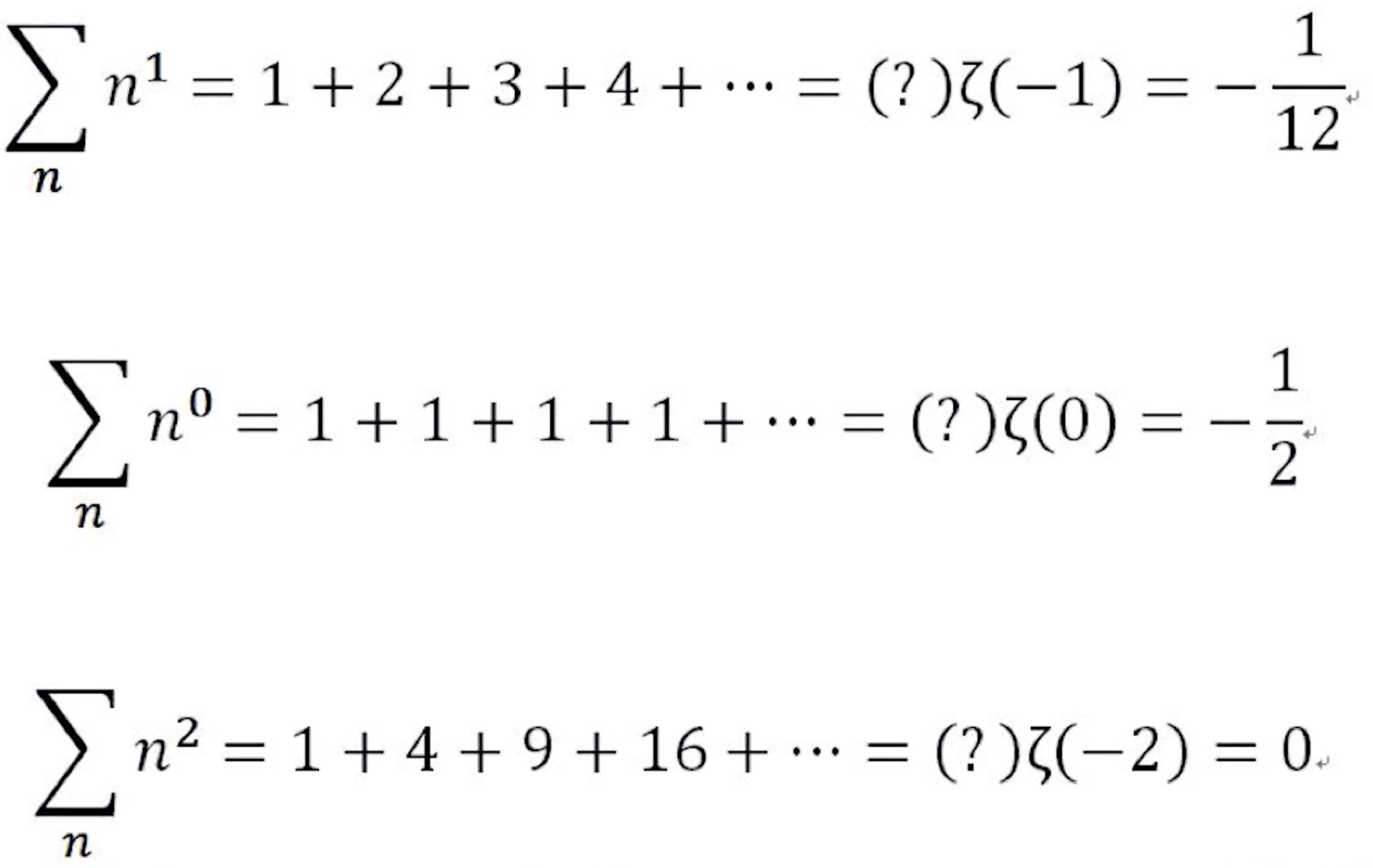
其中第一项含有全体自然数之和,也含有$\zeta(-1)$,也就是标题中提出的问题
在每个等式中都加了问号,是强调这并不是真的相等,只是一种联想
黎曼$\zeta(s)$:复变函数
黎曼将自变量s理解为复数,经过解析延拓之后,最终变成了这样:
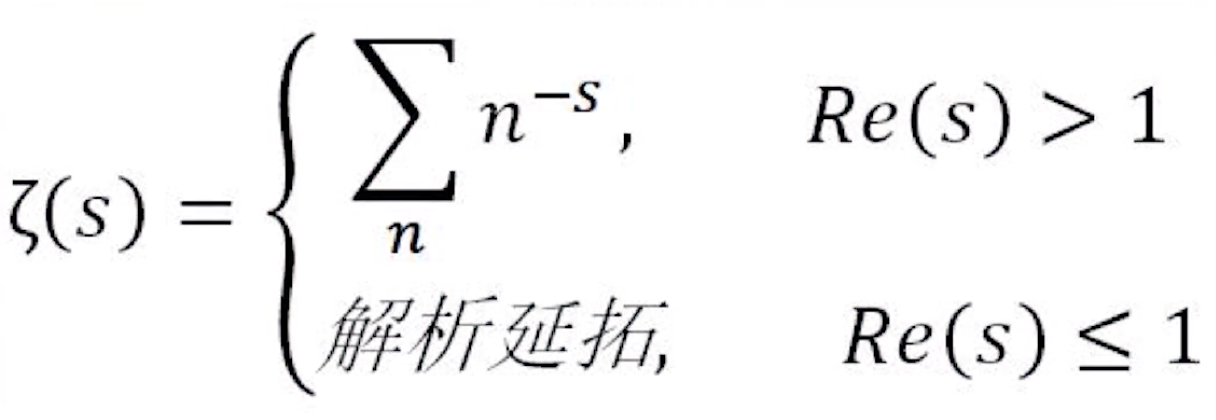
Re表示实部,Im表示虚部
在整个复平面上,黎曼$\zeta$函数只在$s=1$这一点没有定义
复数相关
欧拉公式
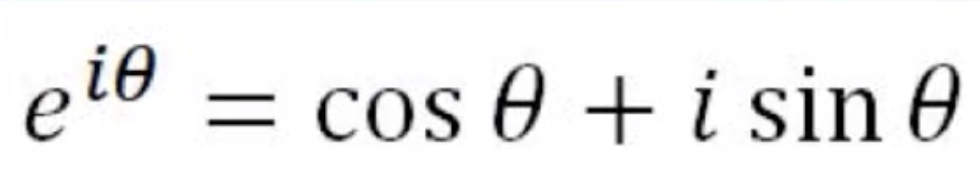
这对应于一个长度为1的矢量,它的方向是从实轴旋转了角度θ
根据欧拉公式,一个底数为实数r、指数为复数(x + yi)的乘方就等于:
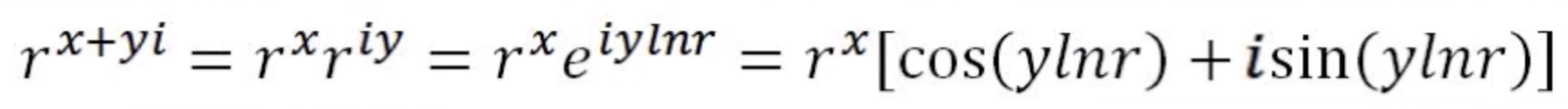
因此,结果矢量的长度只与指数的实部x有关,与指数的虚部y无关;而它的方向只与y有关,与x无关
也就是说,如果给指数加上一个纯虚数,就相当于给乘方的结果做了一个旋转
如果给指数加上一个实数,就相当于改变了乘方矢量的长度,而方向不变
而如果给指数加上一个实部和虚部都不等于0的复数,乘方的结果就是既改变大小,也改变方向
复变函数相关
黎曼把ζ函数的自变量s从实数扩展到了复数,也就是说把ζ函数从实变函数变成了复变函数
好处在于:某种意义上,二维的复变函数比一维的实变函数简单
因为在数轴上接近一个点,只有两个方向,左和右,而在复平面上接近一个点,却有无穷多个方向,例如左边、右边、上边、下边以及任意倾斜的方向
突然想到xz和我说的,函数在某一点可导意味着左导数等于右导数
如果对无穷多个方向做计算都能得到同一个结果,那么这是一个非常强的限制条件,能通过这样的限制条件的复变函数就很容易处理
例如,复变函数的解析延拓就比实变函数的解析延拓容易得多
因此数学界有这样的笑谈:实变函数处理的都是性质非常恶劣的函数,复变函数处理的都是性质非常良好的函数。
可以说,黎曼对$\zeta$函数进行了降维打击
复变函数的零点
复变函数的一个特点是:许多性质都是由它的零点(zero)决定的
例如$±i$就是复变函数$f(z)=z^2+1$的两个零点
如果复平面上围着一个零点做一条曲线,然后求函数在这条曲线上的积分,会发现积分结果完全由零点的性质决定,跟曲线的具体情况没有关系
我们只需要知道函数在零点附近的行为就够了
非平凡零点
首先,黎曼得出了一个等式…
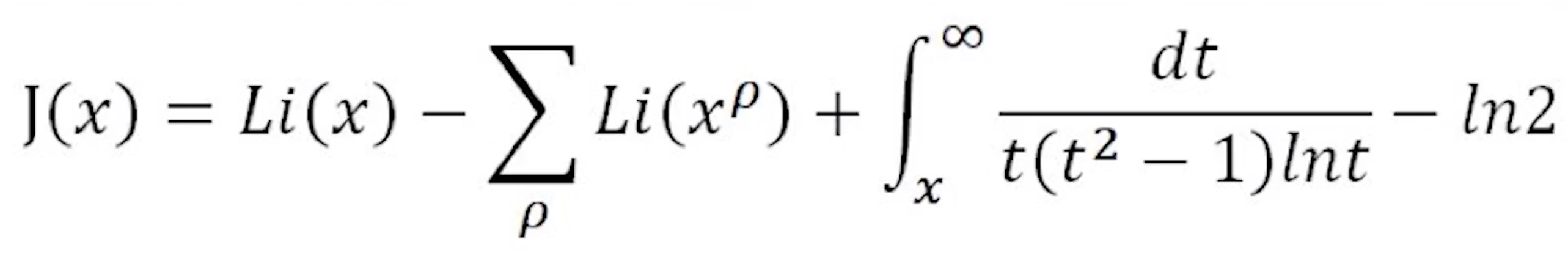
左边的$J(x)$是一个阶梯函数,它在x = 0的地方取值为0,然后每经过一个质数(例如2、3、5)就增加1,每经过一个质数的平方(例如4、9、25)就增加$\frac{1}{2}$,每经过一个质数的三次方(例如8、27、125)就增加$\frac{1}{3}$,以此类推,每经过一个质数的n次方就增加$\frac{1}{n}$
可以理解为,一个质数的n次方被算作了$\frac{1}{n}$个质数
显然,这个函数跟质数的分布密切相关
等式右边的第一项$Li(x)$叫做对数积分函数(logarithmic integralfunction),定义为:
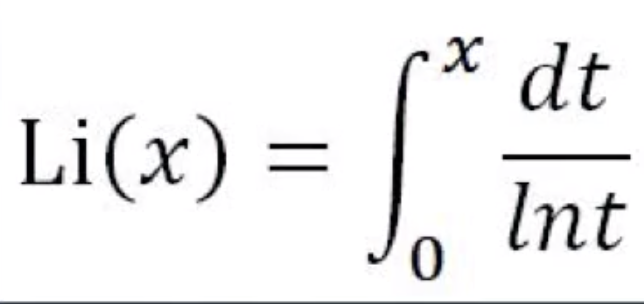
在x很大的时候,$Li(x)≈\frac{x}{ln(x)}$
右边的第二项的函数形式仍然是对数积分函数,但是自变量是所有x的ρ次方
这里的ρ是黎曼$\zeta$函数的非平凡零点(non-trivial zeroes)
关于非平凡的解释:
黎曼证明了,s等于-2、-4、-6、-8等负的偶数值的时候,$\zeta(s)$必然等于0
如果用类似于全体自然数的和等于$-\frac{1}{12}$的语言来描述,那么全体自然数的偶数次方和等于0
在数学家们看来,这是显然的,于是他们把$\zeta$函数的这种零点叫做平凡零点(trivial zeroes)
从高中数学竞赛的角度,显然,平凡,乏趣这三个词是等价的
可以确定的是,非平凡零点肯定不在实轴上;也就是说,实轴上除了负偶数,没有其它零点
也许会问,既然非平凡零点ρ不是实数,那么x的ρ次方也不是实数,如何计算虚数自变量的对数积分函数?
回答是:数学家又做了一个解析延拓,把对数积分函数的定义域扩展到了复数。
总之,黎曼对一个与质数分布密切相关的函数$J(x)$给出了一个表达式,其中唯一不清楚的部分来自黎曼$\zeta$函数的非平凡零点
质数计数函数
质数计数函数(prime-counting function),意为小于等于给定数值x的质数个数,经常写作$\pi(x)$
不过这个名字和圆周率没什么关系
显然,如果我们对质数计数函数知道了一个简便的计算公式,那么对第n个质数也就有了快速的算法
黎曼得到的并不是$\pi(x)$而是$J(x)$,不过这两个函数包含的信息是等价的
在这个意义上,质数分布的全部信息都包含在黎曼$\zeta$函数非平凡零点的位置之中
其中$\pi(x)$和$J(x)$具体的关系是:
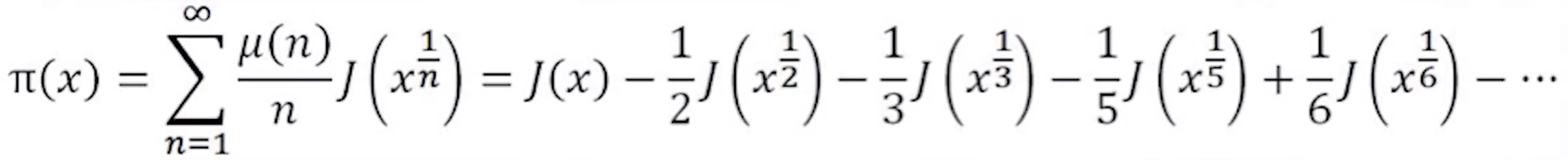
其中$\mu(n)$叫做莫比乌斯函数(Möbius function)
没错,就是莫比乌斯带的那个人
莫比乌斯函数的取值只有三种可能:0和±1
1、如果n可以被任何一个质数的平方整除,也就是说在它的质因数分解中有一个质因数出现了二次或更高次方,那么$\mu(n)=0$
2、如果n不能被任何一个质数的平方整除,也就是说n的任何一个质因数都只出现一次,那么我们来数质因数的个数
(1)假如质因数有偶数个,那么$\mu(n) = 1$,包括了n = 1的情况,因为它没有质因数,0算作偶数,所以μ(1) = 1
(2)假如质因数有奇数个,那么$\mu(n) = -1$
由此可见,$\mu(1) = 1,\mu(2) = -1,\mu(3) = -1,\mu(4) = 0,\mu(5) = -1,\mu(6) = 1$
回到上式,显然$J(x)$是一个增函数,展开式中,随着n的增加,$x^{\frac{1}{n}}$变得越来越小,相应的第n项也变得越来越小
因此,对$\pi(x)$贡献最大的就是第一项
而对$J(x)$贡献最大的是哪一项?
这涉及黎曼$\zeta$函数非平凡零点的位置
临界带和临界线
一个非平凡零点ρ的实部和虚部常被记为σ和t,即ρ = σ + it
黎曼很快就证明了,ρ不可能出现在$σ > 1$或者$σ < 0$的位置
也就是说,非平凡零点只可能出现在$0 ≤ σ ≤ 1$的区域里
在复平面上,这对应一条宽度为1的竖直条带,称为临界带(critical strip)
然后,根据黎曼$\zeta$函数的形式,很容易发现零点对于实轴是对称的
这表明,如果σ + it是一个零点,那么它的共轭复数σ - it也是一个零点,因此,非平凡零点总是上下成对出现的
当我们说第n个非平凡零点的时候,指的总是第n个虚部为正数的非平凡零点,而虚部为负数的那些自然就知道了
再然后,根据黎曼的函数方程,即$\zeta(s)$与$\zeta(1 – s)$之间的联系,又很容易发现,非平凡零点对于$σ = \frac{1}{2}$这条竖线是对称的
这表明,如果σ + it是一个零点,那么1 - σ + it也是一个零点。
黎曼猜想
黎曼计算了几个非平凡零点的位置,发现它们的实部都等于$\frac{1}{2}$
例如第一、二、三个非平凡零点,实部都等于$\frac{1}{2}$,而虚部分别约等于14.1347、21.0220和25.0109
然后,他就做出了一个猜想:
黎曼$\zeta$函数所有的非平凡零点,实部都等于$\frac{1}{2}$
我们把$σ = \frac{1}{2}$的这条竖线称为临界线(critical line),也就是临界带的中心线
我们已经知道,所有的非平凡零点都在临界带里,但黎曼猜想却大大加强了这个结论,它猜测:所有的非平凡零点都在临界线上!
至今还没有被普遍接受的证明或证伪,但是数值计算的结果为黎曼猜想提供了强有力的支持
已经计算了十万亿个非平凡零点,都符合这一猜想
质数定理
随着数字的增大,质数一般而言会变得越来越稀疏
高斯发现质数分布的密度大约是对数函数的倒数
一百多年后终于被证明了,从此被称为质数定理(prime number theorem)
不过在方法论上,质数定理却只是研究黎曼猜想的一个中间产物
黎曼一开始就证明了:黎曼$\zeta$函数的非平凡零点只能出现在$0 ≤ σ ≤ 1$的临界带里
对于质数定理而言,棘手的就是那两个等于号,如果能去掉等于号,也就是把临界带去掉两条$σ = 0$和$σ = 1$的边界,让非平凡零点只能出现在临界带的内部而不是左右边界上,那么质数定理立刻就得证了
因为这时很容易证明,对质数计数函数$\pi(x)$的主要贡献来自对数积分函数$Li(x)$,次要贡献来自黎曼$\zeta$函数的所有非平凡零点
在黎曼的论文发表37年后,两条边终于被去掉了…
因此,质数定理和黎曼猜想的难度有数量级的差距
质数定理的内容,其实就是小于等于x的质数个数$\pi(x)≈Li(x)$
严格地说,当x趋于无穷时,两者比值趋于1
已经提高,在x很大时,$Li(x)≈\frac{x}{ln(x)}$,因此质数定理也可以表述为$\pi(x)\approx\frac{x}{ln(x)}$
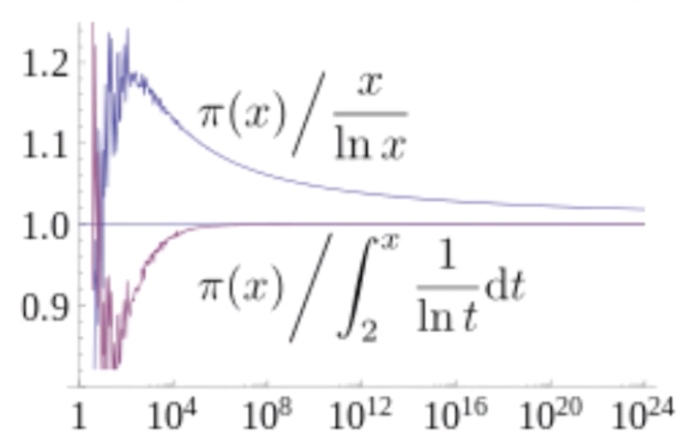
从图中可以发现,随着x的增大,$\pi(x)$与这两种近似表达式的比例都趋于1
不过作为对$\pi(x)$的近似,Li(x)要好得多,不过这只是定量的区别,不是定性的区别
用密度的语言说,在x附近的一个自然数是质数的概率,大约是$\frac{1}{ln(x)}$。同时,在小于等于x的自然数中任选一个是质数的概率,也大约是$\frac{1}{ln(x)}$
由此可见,质数定理构成了我们对质数分布的基础描述
而黎曼猜想表征的就是对这个基础描述的修正
再次重复,质数分布的全部信息都包含在黎曼$\zeta$函数的非平凡零点的位置之中
看到一段评论
质数定理,相当于有人给你打了每句歌词字幕轴;
非平凡零点就是有人把文字填进去了;
而黎曼猜想是进一步打出了带特效的歌词时间轴。