haskell学习

发表于 | 阅读次数:

sth.

装载调用

1
doubleMe x = x + x

保存为test.hs，命令行中:l test.hs

1
2
3
4
5
Prelude> :l test.hs 
[1 of 1] Compiling Main             ( test.hs, interpreted )
Ok, modules loaded: Main.
*Main> doubleMe 9
18

多个参数

1
2
3
4
doubleUs x y = x*2 + y*2

*Main> doubleUs 1 2
6

if

if强制要求有else，正因如此，if语句一定会返回某个值，所以if语句也是一个表达式

1
2
3
4
5
doubleSmallNumber x = if x > 100
    then x
    else x*2

doubleSmallNumber' x = (if x > 100 then x else x*2)

所以把if语句置于一行会更好理解

其中单引号是函数命名的合法字符，可以用来区分一个稍经修改但差别不大的函数

无参函数(定义)

1
2
3
4
vct'purecall = "no_para_func"

*Main> vct'purecall
"no_para_func"

首字母大写的函数是不允许的

没有参数的函数通常被称作定义，这里vct'purecall就和字符串no_para_func等价，且它的值不可被修改

List

ghci中，可以用let关键字定义一个常量

ghci中执行let a = 1与脚本中的a = 1是等价的

1
2
3
4
5
6
*Main> let lostNumbers = [4,8,15,16,23,48]
*Main> lostNumbers 
[4,8,15,16,23,48]

*Main> ['a','b']
"ab"

List中不能同时出现字符和数字

字符串实际上就是一组字符的List，”test”实际上是[‘t’,’e’,’s’,’t’]的语法糖

通过++运算符可以合并List

1
2
3
4
*Main> [1,2,3] ++ [5]
[1,2,3,5]
*Main> "hello" ++ " " ++ "world"
"hello world"

也可以用:运算符，[1,2,3] 实际上是1:2:3:[]的语法糖，表示一个空List从前端插入元素

1
2
3
4
*Main> 'A':" SMALL CAT"
"A SMALL CAT"
*Main> 4:[1,3,5]
[4,1,3,5]

按照索引取得List中的元素，使用!!运算符

1
2
3
4
*Main> [3.1,3.14,3.1415] !! 1
3.14
*Main> "hello" !! 0
'h'

List作为List元素

1
2
3
4
5
*Main> let b = [[1,2,3,4],[7,8,9]]
*Main> b
[[1,2,3,4],[7,8,9]]
*Main> b ++ [[-1,-2]]
[[1,2,3,4],[7,8,9],[-1,-2]]

> >=依次比较List元素的大小

1
2
*Main> [3,1,2]>[2,3,3]
True

head返回头部，tail返回尾部(除去头部的部分)，last返回最后一个元素，init返回除去最后一个元素的部分(为什么叫init…)，在使用这些时要特别注意空List，错误不会在编译期被捕获

如果我们把List想象成一只怪兽，就是这个样子

1

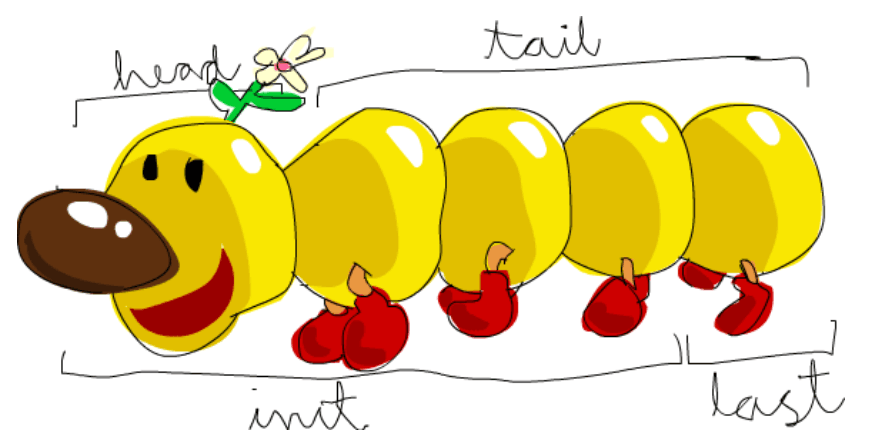
length返回长度，null检查是否为空，reverse反转，take返回一个List的前几个元素，drop从返回第x个元素开始的List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
*Main> head [5,4,3,2,1]
5
*Main> tail [1,2,3,4,5,6]
[2,3,4,5,6]
*Main> last [2,3,4]
4
*Main> init [3,4,5]
[3,4]
*Main> length ['z','x','v']
3
*Main> null [1,2,3]
False
*Main> null []
True
*Main> reverse ['t','e','m','p']
"pmet"
*Main> take 3 [1,2,3,4,5]
[1,2,3]
*Main> take 6 [1,2,3,4,5]
[1,2,3,4,5]
*Main> take 0 [1,5]
[]
*Main> drop 2 [1,2,3,4,5]
[3,4,5]
*Main> drop (-1) [1,2,3,4,5]
[1,2,3,4,5]
*Main> drop 6 [1,2,3,4,5]
[]

maximum和minimum分别返回最大值和最小值，sum返回所有元素的和，product返回所有元素的乘积

elem判断元素是否包含于一个List，通常以中缀函数形式调用它

1
2
3
4
5
6
7
8
9
10
11
12
*Main> maximum [1,2,3]
3
*Main> minimum  [1,2,3]
1
*Main> sum [3,4,5]
12
*Main> product  [3,4,5]
60
*Main> elem 4 [1,2,3,5]
False
*Main> 4 `elem` [1,4]
True

range

range简单使用：

1
2
3
4
5
6
Prelude> [1..20]
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]
Prelude> ['a'..'z']
"abcdefghijklmnopqrstuvwxyz"
Prelude> ['K'..'Z']
"KLMNOPQRSTUVWXYZ"

还支持指定每一步该跨多远，比如，求1到20间的所有偶数或3的倍数

1
2
3
4
Prelude> [2,4..20]
[2,4,6,8,10,12,14,16,18,20]
Prelude> [3,6..20]
[3,6,9,12,15,18]

不能通过[1,2,4..100]这样的语句来获得所有2的幂

[20..1]也是不行的，必须要[20,19..1]

如果使用浮点数，由于定义原因，它并不精确

1
2
Prelude> [0.1,0.2..1]
[0.1,0.2,0.30000000000000004,0.4000000000000001,0.5000000000000001,0.6000000000000001,0.7000000000000001,0.8,0.9,1.0]

应该尽量避免在range中使用浮点数

也可以不标明range的上限，从而得到一个无限长度的List

考虑取前8个13的倍数：

1
2
3
4
Prelude> [13,26..13*8]
[13,26,39,52,65,78,91,104]
Prelude> take 8 [13,26..]
[13,26,39,52,65,78,91,104]

后一种是更好的写法

由于haskell是惰性的，它不会对无限长度的List求值

它会看你从它那去多少，在这里它看见你只要8个元素，便欣然交差

如下是几个生成无限 List 的函数 cycle 接受一个 List 做参数并返回一个无限 List，划好范围

1
2
3
4
5
6
Prelude> take 10 (cycle [1,2,3])
[1,2,3,1,2,3,1,2,3,1]
Prelude> take 7 (cycle "NULL ")
"NULL NU"
Prelude> take 15 (cycle "NULL ")
"NULL NULL NULL "

repeat接受一个值作参数，并返回一个仅包含该值的无限List，与用cycle处理单元素List差不多

1
2
3
4
Prelude> take 10 (repeat 5)
[5,5,5,5,5,5,5,5,5,5]
Prelude> take 10 (repeat 'x')
"xxxxxxxxxx"

不过若只是想得到包含相同元素的List，用replicate会更简单

1
2
Prelude> replicate 3 10
[10,10,10]

List Comprehension

数学中，集合(Set Comprehension) 概念中的comprehension

通过它，可以从既有的集合中按照规则产生一个新的集合，

比如前十个偶数的集合可以表示为：

竖线左边是输出函数，x是变量，N是输入集合

在haskell中，取前10个偶数

1
2
Prelude> [x*2 | x <- [1..10]]
[2,4,6,8,10,12,14,16,18,20]

如果只想取乘2以后大于等于12的元素

1
2
Prelude> [x*2 | x <- [1..10], x*2>=12]
[12,14,16,18,20]

逗号后是限制条件(predicate)

再考虑50到100中，所有除以7余3的元素

1
2
Prelude> [x | x <- [50..100], x `mod` 7 == 3]
[52,59,66,73,80,87,94]

从一个List中筛选出符合特定限制条件的操作也可以称为过滤(flitering)

再举个例子，把List中所有大于10的奇数变为”BANG”，小于10的奇数变为”BOOM”，其它都扔掉

考虑重用，我们将这个comprehension置于一个函数中

1
boomBans xs = [ if x < 10 then "BOOM" else "BANG" | x <- xs,odd x]
1
2
*Main> boomBans [7..13]
["BOOM","BOOM","BANG","BANG"]

也可以加多个限制条件，比如获得10到20中所有不等于13,15或19的数

1
2
*Main> [x | x <- [10..20], x/=13, x/=15, x/=19]
[10,11,12,14,16,17,18,20]

还可以从多个列表中取元素，这样comprehension会把所有的元素组合交付给输出函数，在不过滤的前提下，2个长度为4的集合的comprehension会产生一个长度为16的List

比如有两个List，[2,5,10]和[8,10,11]，要取它们所有组合的积

1
2
*Main> [x*y | x <- [2,5,10], y <- [8,10,11]]
[16,20,22,40,50,55,80,100,110]

再取乘积大于50的结果

1
2
*Main> [x*y | x <- [2,5,10], y <- [8,10,11], x*y > 50]
[55,80,100,110]

我们取一组名词和形容词的List comprehension，写诗的话可能用得着

1
2
3
4
5
6
*Main> let nouns = ["hobo","frog","pope"]
*Main> let adjectives = ["lazy","grouchy","scheming"]

*Main> [adjective ++ " " ++ noun | adjective <- adjectives ,noun <- nouns]
["lazy hobo","lazy frog","lazy pope","grouchy hobo","grouchy frog",
"grouchy pope","scheming hobo","scheming frog","scheming pope"]

最后再写一个自己的length函数，命名为length'

1
length' xs = sum [1 | _ <- xs]

其中_表示我们不关心从List中取什么值，这个函数将List中的所有元素置换为1，并且相加求和

字符串也是List，完全可以使用list comprehension来处理字符串

除去字符串中所有非大写字母

1
removeNonUppercase st = [c | c <- st , c `elem` ['A'..'Z']]
1
2
*Main> removeNonUppercase "Hello,World"
"HW"

其中，限制条件做了所有的工作，只有在['A'..'Z']之间的字元才可以被包含

若操作含有List的List，可以嵌套使用list comprehension

在不拆开它的前提下除去其中所有的奇数

even 偶数

1
2
3
*Main> let xxs = [[1,2,3,4,5],[4,5,6,7,8],[1,2,1,3,4,5,6,7,7]]
*Main> [ [ x | x <- xs ,even x] | xs <- xxs ]
[[2,4],[4,6,8],[2,4,6]]

Tuple

如果要表示二维向量，可以使用List，但考虑将一组向量置于一个List中来表示平面图形

类似[[1,2],[8,11],[4,5]]是可以的，但仍有问题：

[[1,2],[8,11,5],[4,5]]也是合法的，因为其中元素的型别都相同，这样编译器并不会报错

然而一个长度为2的Tuple(也可以称为Pair)是一个独立的类型，这就意味着一个包含一组序对的List不能再加入一个三元组，所以把原先的[ ] 改为( )会更好

[(1,2),(8,11),(4,5)]

如果尝试[(1,2),(2,3,4),(4,4)]就会报错

使用Tuple前应该明确一条数据中应该有多少个项，每个Tuple都是独立的型别，不能给它追加元素

唯一能做的是给一个List追加序对，三元组等内容

fst返回一个序对的首项，snd返回尾项（不能与应用与三元组等）

zip函数，可以用于生成一组序对的List，在需要组合或者遍历两个List时很有用

1
2
*Main> zip [1..5]['a'..'e']
[(1,'a'),(2,'b'),(3,'c'),(4,'d'),(5,'e')]

如果两个List不一样长，较长的List会在中间断开

由于haskell是惰性的，因此可以处理有限和无限的List也是可以的

1
2
*Main> zip [1..]['x'..'z']
[(1,'x'),(2,'y'),(3,'z')]

考虑一个问题，同时应用List和Tuple

如何取得三边长度皆为整数，且小于等于10

并且周长为24的直角三角形

1
*Main> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10]]

列出所有三边的可能，再加上直角的条件

1
2
3
*Main> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..10], a <- [1..10], a^2 + b^2 == c^2] 
*Main> triangles 
[(4,3,5),(3,4,5),(8,6,10),(6,8,10)]

这里我们规定$ a<=b<=c $

再加上周长为24的条件

1
2
3
*Main> let triangles = [ (a,b,c) | c <- [1..10], b <- [1..c], a <- [1..b], a^2 + b^2 == c^2 , a+b+c == 24] 
*Main> triangles 
[(6,8,10)]

这就是函数式语言的一般思路：先取一个初始的集合并将其变形，执行过滤条件，最后取得正确结果

类型&类型类

类型相关

haskell是静态类型的，也支持类型推导

可以用ghci来检测表达式的类型，用:t命令加任何可用的表达式

1
2
3
4
5
6
7
8
9
10
*Main> :t 'a'
'a' :: Char
*Main> :t True
True :: Bool
*Main> :t "Hello"
"Hello" :: [Char]
*Main> :t (False,'x')
(False,'x') :: (Bool, Char)
*Main> :t 4 == 5
4 == 5 :: Bool

可见，:t命令处理表达式的输出结果为：表达式 + :: + 其类型，其中::读作它的类型为

1
2
addThree :: Int -> Int -> Int -> Int
addThree x y z = x + y + z

addThree带有三个整形参数，返回值是整形

前三个表示参数，最后一个表示返回值

同样也可以用:t检测函数类型

1
2
*Main> :t addThree 
addThree :: Int -> Int -> Int -> Int

Integer`也表示整数，差别在于它是无界的

1
2
factorial :: Integer -> Integer
factorial n = product [1..n]
1
2
*Main> factorial 50
30414093201713378043612608166064768844377641568960512000000000000

类型的首字母必是大写

考虑head函数的类型，它可以取任何List的首项

1
2
*Main> :t head
head :: [a] -> a

a是小写，所以它不是类型，而是类型变量，可以是任意的类型，和泛型(generic)很相似

使用到类型变量的函数被称作多态函数

在命名上，类型变量使用多个字符是合法的，不过约定俗成通常都是使用单个字符

再考虑fst函数，取一个包含两个类型的Tuple作为参数，并以第一个项的类型作为返回值

1
2
3
*Main> :t fst
fst :: (a, b) -> a
*Main>

注意，a和b是不同的类型变量，可以是不同的类型，它只是标明了首项的类型和返回值的类型相同

类型类

类型定义行为的接口，如果一个类型属于某类型类，那它必实现了该类型类所描述的行为

可以看做是java中接口(interface)的类似物

考虑 == 函数的类型声明

1
2
*Main> :t (==)
(==) :: Eq a => a -> a -> Bool

判断相等的 == 运算符是函数，+-*/之类的运算符也是同样

默认情况下它们多为中缀函数

若要查看它的类型，就必须得用括号使其作为另一个函数，或者说以前缀函数的形式调用它

这里的=>符号，左边的部分叫做类型约束

可以这样读相等函数取两个相同类型的值作为参数并返回一个布尔值，而这两个参数的类型同在Eq类中(即类型约束)

Eq这一类型类提供了判断相等性的接口，凡是可比较相等性的类型必属于Eq类

elem函数类型为(Eq a)=>a->[a]->Bool

1
2
*Main> :t elem
elem :: (Eq a, Foldable t) => a -> t a -> Bool

检测值是否存在于一个List时用到了==函数

几个基本的类型类

Eq

Eq包含可判断相等性的类型，提供实现的函数是 == 和/=

所以，只要一个函数有Eq类的类型限制，那么它必定在定义中用到了==和/=

因为除函数以外的所有类型都属于Eq，所以它们都可判断相等性

Ord

Ord包含可比较大小的类型

compare函数取两个Ord类中的相同类型的值作为参数，返回比较的结果

其结果是如下三种类型之一： GT LT EQ

1
2
*Main> :t (>)
(>) :: Ord a => a -> a -> Bool

类型若要成为Ord的成员，必先加入Eq家族

1
2
3
4
5
6
7
8
*Main> "hello"<"world"
True
*Main> "hello" `compare` "world"
LT
*Main> 5 >= 2
True
*Main> 5 `compare` 2
GT

Show

Show的成员为可用字符串表示 的类型

操作Show类型类，最常用的函数是show，它可以取任一Show的成员类型并将其转为字符串

1
2
3
4
5
6
*Main> show 3
"3"
*Main> show 3.14
"3.14"
*Main> show True
"True"

Read

Read是与Show相反的类型类，它可以将一个字符串转为Read的某成员类型

1
2
3
4
5
6
*Main> read "True" || False
True
*Main> read "8.2" + 3.8
12.0
*Main> read "[1,2,3,4]" ++ [3] 
[1,2,3,4,3]

尝试read "4"，这里和我本地不太一样

1
2
3
4
5
ghci> read "4"   
< interactive >:1:0:   
    Ambiguous type variable `a' in the constraint:   
      `Read a' arising from a use of `read' at :1:0-7   
    Probable fix: add a type signature that fixes these type variable(s)

ghci说它不清楚我们想要的是什么样的返回值

注意调用read后的部分，ghci通过它来判断类型

这里它只知道我们要的类型属于Read类型类，而不能明确到底是哪个

1
2
*Main> :t read
read :: Read a => String -> a

它的返回值属于Read类，但我们若用不到这个值，它就永远不会得知该表达式的类型

所以我们需要在一个表达式后加上::的类型注释，以明确其类型，如下：

1
2
3
4
5
6
7
8
*Main> read "5" :: Int
5
*Main> read "5" :: Float
5.0
*Main> read "[1,2,3,4]" :: [Int]
[1,2,3,4]
*Main> read "(3,'a')" :: (Int,Char)
(3,'a')

Enum

Enum的成员都是连续的类型，也就是可枚举

主要好处在于，我们可以在Range中用到它的成员类型：每个值都有后继(successer)和前驱(predecesor)，分别可以通过succ和pred函数得到

该类型类包含的类型有：()，Bool，Char，Ordering，Int，Integer，Float和Double

1
2
3
4
5
6
7
8
Prelude> ['a'..'e']
"abcde"
Prelude> [LT .. GT]
[LT,EQ,GT]
Prelude> [3 .. 5]
[3,4,5]
Prelude> succ 'B'
'C'

Bounded

Bounded的成员都有一个上限和下限

1
2
3
4
5
6
7
8
9
10
11
12
Prelude> minBound :: Int
-9223372036854775808
Prelude> maxBound :: Int
9223372036854775807
Prelude> maxBound :: Bool
True
Prelude> minBound :: Bool
False
Prelude> minBound :: Char
'\NUL'
Prelude> maxBound :: Char
'\1114111'

minBound和maxBound函数的类型都是(Bounded a) => a，可以认为它们都是多态常量

1
2
Prelude> :t minBound 
minBound :: Bounded a => a

如果其中的项都属于Bounded类型类，那么该Tuple也属于Bounded

1
2
Prelude> maxBound :: (Bool,Int,Char)
(True,9223372036854775807,'\1114111')

Num

表示数字的类型类，它的成员类型都具有数字的特征

检查一个数字的类型：

1
2
Prelude> :t 20
20 :: Num a => a

看起来所有的数字都是多态常量，它可以作为所有Num类型类中的成员类型

检查*运算符的类型，可以发现它可以处理一切数字

1
2
Prelude> :t (*)
(*) :: Num a => a -> a -> a

它只取两个相同类型的参数，所以以下会报错

(5 :: Int) * (6 :: Integer)

这样是可以的5 * (6 :: Integer)

类型只有亲近Show和Eq，才可以加入Num

Integral

同样是表示数字的类型类，Num包含所有的数字：实数和整数

而Integral仅包含整数，其中的成员类型有Int和Integer

Floating

Floating仅包含浮点类型：Float和Double

函数语法

模式匹配

简单例子，检查传入的数字是不是7

1
2
3
lucky :: (Integral a) => a -> String
lucky 7 = "number 7"
lucky x = "not 7"

在调用lucky时，模式会从上至下进行检查，一旦有匹配，那对应的函数体就被应用了

这个模式唯一匹配的参数是7，如果不是7，就跳转到下一个模式，它匹配一切数值并将其绑定为x

稍复杂一些

1
2
3
4
5
6
7
sayMe :: (Integral a) => a -> String   
sayMe 1 = "One!"   
sayMe 2 = "Two!"   
sayMe 3 = "Three!"   
sayMe 4 = "Four!"   
sayMe 5 = "Five!"   
sayMe x = "Not between 1 and 5"

注意，如果把最后匹配一切的模式移到最前，那么结果就都是Not between 1 and 5了

阶乘(递归)

1
2
3
factorial :: (Integral a) => a -> a   
factorial 0 = 1   
factorial n = n * factorial (n - 1)

若是把第二个模式放在前面，就会捕获包括0在内的一切数字，这样计算就永远不会停止

它总是优先匹配最符合的那个，最后才匹配万能的

模式匹配也会失败，例如：

1
2
3
4
charName :: Char -> String   
charName 'a' = "Albert"   
charName 'b' = "Broseph"   
charName 'c' = "Cecil"

用没有考虑到的字符去调用它

1
2
3
4
5
6
ghci> charName 'a'   
"Albert"   
ghci> charName 'b'   
"Broseph"   
ghci> charName 'h'   
"*** Exception: tut.hs:(53,0)-(55,21): Non-exhaustive patterns in function charName

这表明，这个模式不够全面

因此，定义模式时，一定要留一个万能匹配的模式，以使程序不会因为不可预料的输入而崩溃

对Tuple也可以进行模式匹配

考虑二维空间的向量相加，如果不了解模式匹配，可能会写出这样的代码

1
2
addVectors :: (Num a) => (a, a) -> (a, a) -> (a, a)   
addVectors a b = (fst a + fst b, snd a + snd b)

有更好的方法，上模式匹配：

1
2
addVectors :: (Num a) => (a, a) -> (a, a) -> (a, a)   
addVectors (x1, y1) (x2, y2) = (x1 + x2, y1 + y2)

考虑之前提到的问题

fst和snd可以从序对中取出元素，三元组该怎么处理？

1
2
3
4
5
6
first :: (a,b,c) -> a
first (x,_,_) = x
second :: (a,b,c) -> b
second (_,y,_) = y_
third :: (a,b,c) -> c
third (_,_,z) = z

这里的_同样表示我们不关心这部分的具体内容

在List Comprehension中使用模式匹配

1
2
3
*Main> let xs = [(1,3),(3,4),(7,9)]
*Main> [a+b | (a,b) <- xs]
[4,7,16]

x:xs这种模式的应用非常广泛，尤其是递归函数

不过它只能匹配长度大于等于1的List

如果要把List的前三个元素都绑定到变量中，可以使用类似x:y:z:xs的形式

它只能匹配长度大于等于3的List

[1,2,3]本质就是1:2:3:[]的语法糖

已经知道了如何对List作模式匹配，现在实现我们自己的head函数

1
2
3
head' :: [a] -> a
head' [] = error "Can't call head on an empty list!"
head' (x:_) = x

注意，要绑定多个变量(用_也是如此)，必须用()括起来

同时注意error函数，它可以生成一个运行时错误，用参数中的字符串表示对错误的描述，并且会使程序直接崩溃

这次用模式匹配和递归重新实现自己的length函数

1
2
3
length' :: (Num b) => [a] -> b
length' [] = 0
length' (_:xs) = 1 + length' xs

先定义好未知输入的结果——空List，也叫做边界条件

再在第二个模式中将这个List分割为头部和尾部

匹配头部用的_，因为我们并不关心它的值

我们顾及了List所有可能的模式，第一个模式匹配空List，第二个模式匹配非空List

再实现sum

我们知道空List的和是0，就把它定义为一个模式，再考虑递归调用

1
2
3
sum' :: (Num a) => [a] -> a
sum' [] = 0
sum' (x:xs) = x + sum' xs

这里我们关心头部的值，所以用的x而不是_

as模式

将一个名字和@置于模式前，可以在按模式分割时仍保留对整体的引用

1
2
3
capital :: String -> String
capital "" = "Empty string!"
capital all@(x:xs) = "The first letter of " ++ all ++ " is " ++ [x]

输出结果：

1
2
*Main> capital "hello"
"The first letter of hello is h"

Guards

一个guard就是一个布尔表达式，通常靠右缩进排成一列

如果为真，就使用对应的函数体，为假就送去下一个guard

1
2
3
4
5
func :: (RealFloat a) => a -> String
func x
    | x <= 10 = "x<10"
    | x <= 20 = "x<=20"
    | otherwise = "x>20"
1
2
3
4
5
6
*Main> func 2
"x<10"
*Main> func 18
"x<=20"
*Main> func 30
"x>20"

也可以传入参数进行运算后得出布尔值

1
2
3
4
5
func2 :: (RealFloat a) => a -> a -> String  
func2 x y  
    | x / y < 1 = "x / y < 1"  
    | x / y < 2 = "x / y < 2"  
    | otherwise = "otherwise"
1
2
*Main> func2 2 3
"x / y < 1"

guard也可以塞在一行里，不过会丧失可读性，仅做展示，重写max'函数

1
2
max' :: (Ord a) => a -> a -> a
max' a b | a > b = a | otherwise = b

最后再实现一个自己的compare函数

1
2
3
4
5
myCompare :: (Ord a) => a -> a -> Ordering
a `myCompare` b
    | a > b     = GT
    | a == b    = EQ
    | otherwise = LT
1
2
*Main> 3 `myCompare` 2
GT

使用反单引号，不仅可以以中缀形式调用函数，也可以在定义函数的时候使用它

关键字Where

1
2
3
4
5
6
7
8
9
10
bmiTell :: (RealFloat a) => a -> a -> String  
bmiTell weight height  
    | bmi <= skinny = "You're underweight, you emo, you!"  
    | bmi <= normal = "You're supposedly normal. Pffft, I bet you're ugly!"  
    | bmi <= fat    = "You're fat! Lose some weight, fatty!"  
    | otherwise     = "You're a whale, congratulations!"  
    where bmi = weight / height ^ 2  
          skinny = 18.5  
          normal = 25.0  
          fat = 30.0

跟在guard后面，最好与竖线缩进一致，可以定义多个名字和函数

这些名字对每个guard都是可见的，避免重复

也只对本函数可见，不会污染其他函数的命名空间

如果我们打算换种方式计算bmi ，只需要进行一次修改即可

并且因为只计算一次，效率也有所提升

Where绑定也可以使用模式匹配

1
2
where bmi = weight / height ^ 2  
      (skinny, normal, fat) = (18.5, 25.0, 30.0)

Where绑定中也可以定义函数

这里实现计算一组bmi的函数

1
2
3
calcBmis :: (RealFloat a) => [(a, a)] -> [a]  
calcBmis xs = [bmi w h | (w, h) <- xs] 
    where bmi weight height = weight / height ^ 2

这里我们因为不能依据参数直接进行计算，比如从传入的List中取出每个序对并计算对应的值，因此我们将bmi搞成一个函数

关键词Let

和Where绑定相似，Let绑定是个表达式，允许在任何位置定义局部变量

依据半径和高度求圆柱体表面积的函数：

1
2
3
4
5
cylinder :: (RealFloat a) => a -> a -> a
cylinder r h = 
    let sideArea = 2 * pi * r * h
        topArea = pi * r^2
    in sideArea + 2 * topArea

let 的格式为 let [bindings] in [expressions]，在let中绑定的名字仅对in部分可见

1
2
*Main> cylinder 1 1
12.566370614359172

和where的差别在于，let绑定本身是表达式，而where绑定是语法结构

1
2
*Main> let a = 9 in a + 1
10

因为是表达式所以可以随处安放

1
2
*Main> [let square x = x * x in (square 5, square 3, square 2)]
[(25,9,4)]

若要在一行中绑定多个名字，可以用分号将其分开

1
2
ghci> (let a = 100; b = 200; c = 300 in a*b*c, let foo="Hey "; bar = "there!" in foo ++ bar)  
(6000000,"Hey there!")

可以在let绑定中使用模式匹配，以便从Tuple中取值等操作

1
2
*Main> (let (a,b,c) = (1,2,3) in a+b+c)
6

C++17结构化绑定？

let绑定也可以放到List Comprehension中

1
2
calcBmis :: (RealFloat a) => [(a, a)] -> [a]  
calcBmis xs = [bmi | (w, h) <- xs, let bmi = w / h ^ 2]

let做的只是绑定名字，还可以继续做过滤

1
2
calcBmis :: (RealFloat a) => [(a, a)] -> [a]  
calcBmis xs = [bmi | (w, h) <- xs, let bmi = w / h ^ 2, bmi <= 20.0]

在 List Comprehension 中我们忽略了 let 绑定的 in 部分，因为名字的可见性已经预先定义好了

注意，在| 和let的中间不能使用bmi，还没有绑定

而竖线前面作为返回结果，是可以用bmi的

把一个 let...in 放到限制条件中也是可以的，这样名字只对这个限制条件可见

在 ghci 中 in 部分也可以省略，名字的定义就在整个交互中可见

1
2
3
4
5
6
7
ghci> let zoot x y z = x * y + z  
ghci> zoot 3 9 2  
29  
ghci> let boot x y z = x * y + z in boot 3 4 2  
14  
ghci> boot  
< interactive>:1:0: Not in scope: `boot'

最后的一点，let是个表达式，定义域限制的很小，因此不能在多个guard中使用

where因为是跟在函数体后面，把主函数体距离型别声明近一些会更易读

case expressions

模式匹配本质上就是 case 语句的语法糖，这两段代码是完全等价的：

1
2
3
head' :: [a] -> a  
head' [] = error "No head for empty lists!"  
head' (x:_) = x
1
2
3
head' :: [a] -> a  
head' xs = case xs of [] -> error "No head for empty lists!"  
                      (x:_) -> x

case表达式的语法结构：

1
2
3
4
case expression of pattern -> result  
                   pattern -> result  
                   pattern -> result  
                   ...

函数参数的模式匹配只能在定义函数时使用，而case表达式可以用在任何地方

1
2
3
4
describeList :: [a] -> String  
describeList xs = "The list is " ++ case xs of [] -> "empty."  
                                               [x] -> "a singleton list."   
                                               xs -> "a longer list."

写成这样是等价的

1
2
3
4
5
describeList :: [a] -> String  
describeList xs = "The list is " ++ what xs  
    where what [] = "empty."  
          what [x] = "a singleton list."  
          what xs = "a longer list."

what xs 应该看作一个函数

递归

实现我们自己的maximum函数，模式匹配和递归的配合使用

1
2
3
4
5
6
7
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs)
    | x > maxTail = x
    | otherwise = maxTail
    where maxTail = maximum' xs

改用max函数，更清楚一些

1
2
3
4
maximum' :: (Ord a) => [a] -> a
maximum' [] = error "maximum of empty list"
maximum' [x] = x
maximum' (x:xs) = max x (maximum' xs)

简明扼要，一个List中的最大值就是它的首元素与尾部中最大值相比较得到的结果

反转List

边界条件是空List，若将一个List分割为头部和尾部，那么它反转的结果就是：反转后的尾部与原先的头部相连所得的List

1
2
3
reverse' :: [a] -> [a]
reverse' [] = []
reverse' (x:xs) = reverse' xs ++ [x]

实现自己的take函数

1
2
3
4
5
take' :: (Num i, Ord i) => i -> [a] -> [a]
take' n _
    | n <= 0    = []
take' _ [] = []
take' n (x:xs) = x : take' (n-1) xs

再实现zip函数，生成一组序对的List

取两个List作参数并将其捆绑在一起，两个边缘条件分别是两者为空List

1
2
3
4
zip' :: [a] -> [b] -> [(a,b)]
zip' _ [] = []
zip' [] _ = []
zip' (x:xs) (y:ys) = (x,y):zip' xs ys

elem函数，比较简单

1
2
3
4
5
elem' :: (Eq a) => a -> [a] -> Bool
elem' a [] = False
elem' a (x:xs)
    | a == x    = True
    | otherwise = a `elem'` xs

快速排序

算法：排过序的List就是令所有小于等于头部的元素在先(它们已经排过了序)，后面是大于头部的元素(同样也排好了序)，代码很好理解

因为定义中有两次排序，所以得递归两次

1
2
3
4
5
6
quicksort :: (Ord a) => [a] -> [a]
quicksort [] = []
quicksort (x:xs) = 
    let smallerSorted = quicksort [a | a <- xs, a <= x]
        biggerSorted = quicksort [a | a <- xs, a > x]
    in smallerSorted ++ [x] ++ biggerSorted

注意，算法定义的动词是 “是”什么 ，而不是 “做”什么，再”做”什么…

这就是函数式编程之美

高阶函数

Curried functions

本质上，haskell的所有函数都只有一个参数

所有多个参数的函数都是Curried functions

执行 max 4 5 时，它首先返回一个取一个参数的函数，其返回值不是 4 就是该参数，取决于谁大

然后，以 5 为参数调用它，并取得最终结果

以下两个函数调用时等价的：

1
2
3
4
*Main> max 4 5
5
*Main> (max 4) 5
5

把空格放到两个东西之间，叫做函数调用，有点像运算符，并且拥有最高的优先顺序

考虑 max 函数的型别： max :: (Ord a) => a -> a -> a

它也可以写作： max :: (Ord a) => a -> (a -> a)

可以读作 max 取一个参数 a，并返回一个函数(就是那个 ->)，这个函数取一个 a 型别的参数，返回一个a

这就是之前提到的，为何只用箭头来分隔参数和返回值型别

这样的优势在于，若以不全的参数来调用某函数，就可以得到一个不全调用的函数

以便构造新的函数

(不全调用的函数)简单例子

1
2
multThree :: (Num a) => a -> a -> a -> a
multThree x y z = x * y * z
1
2
3
4
5
6
*Main> let multTwoWithNine = multThree 9
*Main> multTwoWithNine 2 3
54
*Main> let multWithEighteen = multTwoWithNine 2
*Main> multWithEighteen 12
216

构造新的函数：考虑一个与100比较大小的函数

1
2
compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred x = compare 100 x

这时注意到=两边都有x，而compare 100会返回一个与100比较的函数，这正是我们想要的

1
2
compareWithHundred :: (Num a, Ord a) => a -> Ordering
compareWithHundred = compare 100

中缀函数的柯里化

中缀函数也可以不全调用，用括号把它和一边的参数括在一起就可以了

1
2
divideByTen :: (Floating a) => a -> a
divideByTen = (/10)
1
2
*Main> divideByTen 100
10.0

其中调用divideByTen 200就是(/10) 200，它和200/10等价

再考虑一个检查字元是否为大写字母的函数

1
2
isUpperAlphanum :: Char -> Bool
isUpperAlphanum = (`elem` ['A'..'Z'])

唯一的例外是-运算符，按照定义，(-4)理应返回一个将参数减4的函数，实际上为了计算方便它表示负4

如果一定要弄个将参数减4的函数，可以像这样

1
2
subtractFour :: (Num a) => a -> a
subtractFour = subtract 4
1
2
*Main> subtractFour 10
6

高阶函数实例

applyTwice

haskell中的函数可以取另一个函数做参数，也可以返回函数

举个例子，我们写一个：取一个函数，并调用它两次的函数

1
2
applyTwice :: (a -> a) -> a -> a
applyTwice f x = f (f x)

注意型别声明，之前很少用到括号，因为(->)是自然的左结合，但是这里括号是必须的

它标明了首个参数是参数和返回值都是a的函数，第二个参数和返回值也都是a

1
2
3
4
5
6
7
8
9
10
*Main> applyTwice (+3) 10
16
*Main> (+3) `applyTwice`  10
16
*Main> app
appendFile  applyTwice
*Main> applyTwice (++ "world") "hello"
"helloworldworld"
*Main> applyTwice (3:) [1]
[3,3,1]

如果函数需要传入一个一元参数，我们可以用不全调用让它剩一个参数，再把它交出去

zipWith

用高阶函数的思想实现标准库中的函数zipWith，它取一个函数和两个List做参数，用相应的元素调用该函数

1
2
3
4
zipWith' :: (a -> b -> c) -> [a] -> [b] -> [c]  
zipWith' _ [] _ = []  
zipWith' _ _ [] = []  
zipWith' f (x:xs) (y:ys) = f x y : zipWith' f xs ys

注意这个函数的型别声明：

第一个参数是一个函数，它取两个参数返回一个值，它们的型别不必相同

第二、三个参数都是列表

最后返回值是一个列表

1
2
3
4
5
6
7
8
ghci> zipWith' (+) [4,2,5,6] [2,6,2,3]  
[6,8,7,9]  
ghci> zipWith' max [6,3,2,1] [7,3,1,5]  
[7,3,2,5]  
ghci> zipWith' (++) ["foo "，"bar "，"baz "] ["fighters"，"hoppers"，"aldrin"]  
["foo fighters","bar hoppers","baz aldrin"]  
ghci> zipWith' (*) (replicate 5 2) [1..]  
[2,4,6,8,10]

命令式语言使用 for、while、赋值、状态检测来实现功能，再包起来留个界面，使之像函数一样调用函数式语言使用高阶函数来抽象出常见的模式，如成对遍历并处理两个 List 或从中筛除不需要的结果

flip

再考虑实现flip函数，它简单地取一个函数作参数并返回一个相似的函数，差别在于它们的两个参数交换顺序

1
2
3
4
ghci> flip' zip [1,2,3,4,5] "hello"  
[('h',1),('e',2),('l',3),('l',4),('o',5)]  
ghci> zipWith (flip' div) [2,2..] [10,8,6,4,2]  
[5,4,3,2,1]

我猜测，正是由于惰性和柯里化的缘故，haskell中的f(g(x))，会先计算函数复合的结果，再用实际参数调用它

map&filter